Question 5 (7 marks):
Mathematics Society of SMK Mulia organized a competition to design a logo for the society.

Diagram 3 shows the circular logo designed by Adrian. The three blue coloured regions are congruent. It is given that the perimeter of the blue coloured region is 20π cm.
[Use π = 3.142]
Find
(a) the radius, in cm, of the logo to the nearest integer,
(b) the area, in cm2, of the yellow coloured region.
Solution:
(a)
(b)

Mathematics Society of SMK Mulia organized a competition to design a logo for the society.

Diagram 3 shows the circular logo designed by Adrian. The three blue coloured regions are congruent. It is given that the perimeter of the blue coloured region is 20π cm.
[Use π = 3.142]
Find
(a) the radius, in cm, of the logo to the nearest integer,
(b) the area, in cm2, of the yellow coloured region.
Solution:
(a)
(b)

Question 6 (6 marks):
Diagram 4 shows the front view of a part of a roller coaster track in a miniature park.
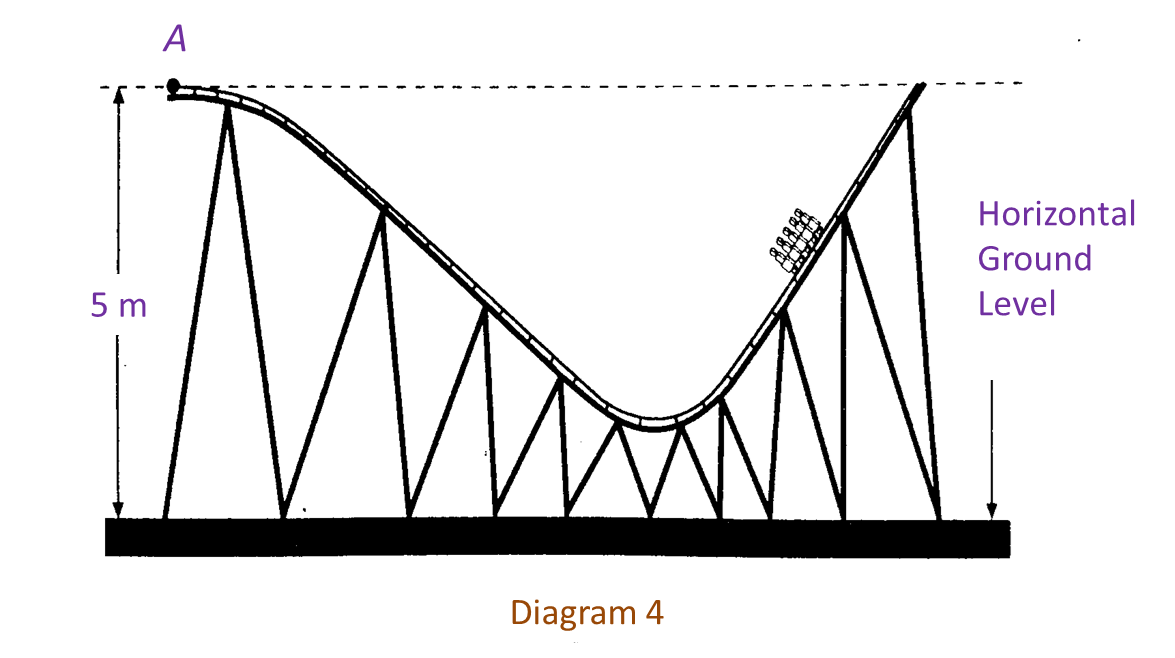
The curve part of the track of the roller coaster is represented by an equation , with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.
Solution:
Diagram 4 shows the front view of a part of a roller coaster track in a miniature park.

The curve part of the track of the roller coaster is represented by an equation , with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.
Solution: