Question 3 (6 marks):
Solution by scale drawing is not accepted.
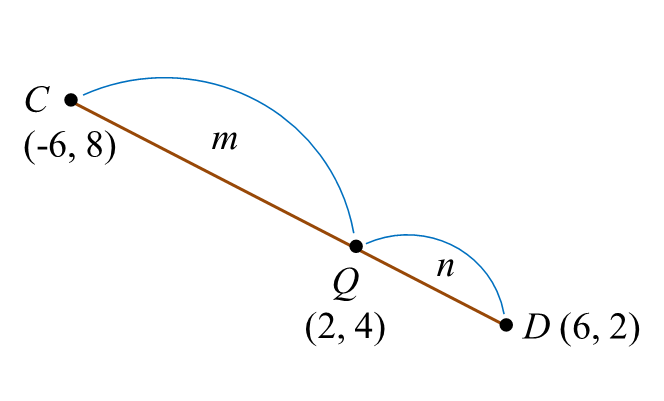
Diagram 1 shows a triangle OCD.
 Diagram 1
Diagram 1
(a) Given the area of triangle OCD is 30 units2, find the value of h.
(b) Point Q (2, 4) lies on the straight line CD.
(i) Find CQ : QD.
(ii) Point P moves such that PD = 2 PQ.
Find the equation of the locus P.
Solution:
(a)
(b)(i)
(b)(ii)
Solution by scale drawing is not accepted.
Diagram 1 shows a triangle OCD.
 Diagram 1
Diagram 1(a) Given the area of triangle OCD is 30 units2, find the value of h.
(b) Point Q (2, 4) lies on the straight line CD.
(i) Find CQ : QD.
(ii) Point P moves such that PD = 2 PQ.
Find the equation of the locus P.
Solution:
(a)
(b)(i)

(b)(ii)
Question 4 (7 marks):
Diagram 2 shows the plan of a rectangular garden ABCD. The garden consists of a semicircular pond ATD and grassy area ABCDT.
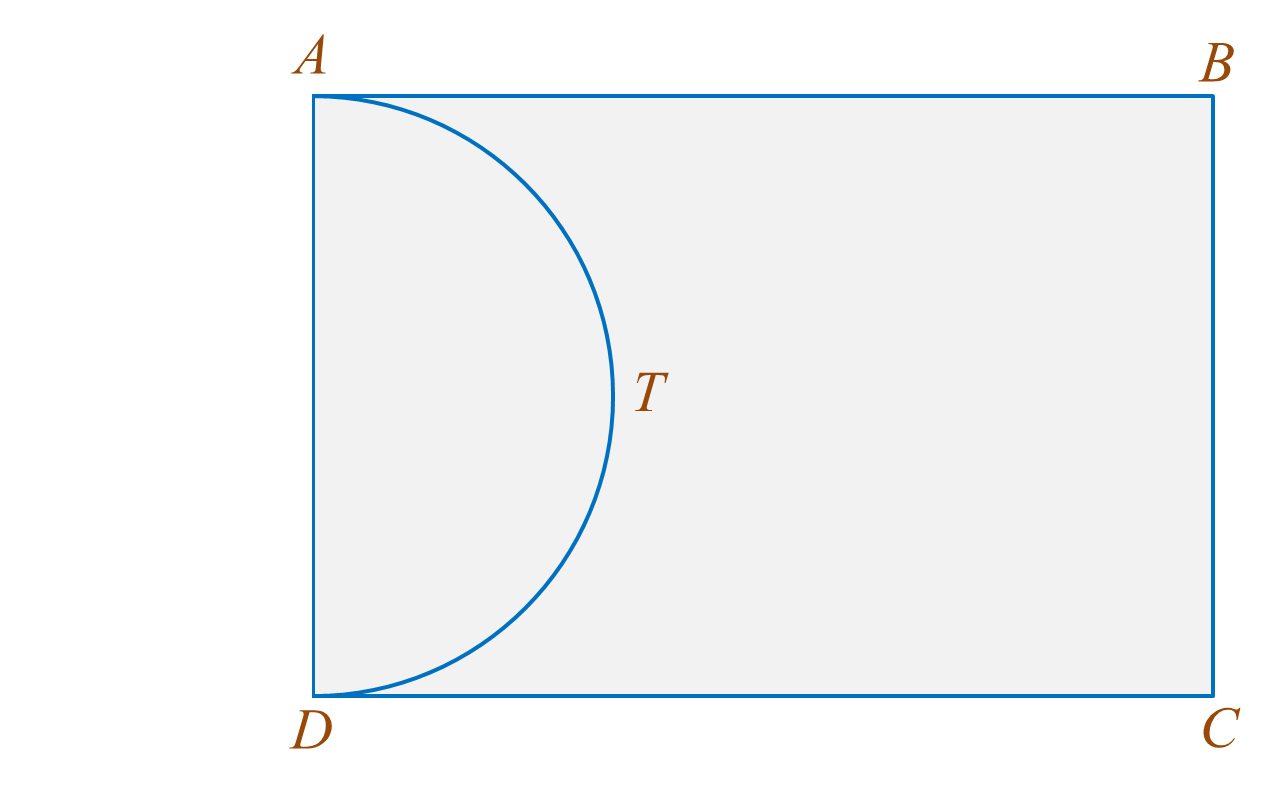 It is given that DC = 6y metre and BC = 7x metre, x ≠ y. The area of the rectangular garden ABCD is 168 metre2 and the perimeter of the grassy area is 60 metre. The pond with uniform depth contains 15.4 metre3 of water.
It is given that DC = 6y metre and BC = 7x metre, x ≠ y. The area of the rectangular garden ABCD is 168 metre2 and the perimeter of the grassy area is 60 metre. The pond with uniform depth contains 15.4 metre3 of water.
By using , find the depth, in metre, of water in the pond.
Solution:
Diagram 2 shows the plan of a rectangular garden ABCD. The garden consists of a semicircular pond ATD and grassy area ABCDT.
 It is given that DC = 6y metre and BC = 7x metre, x ≠ y. The area of the rectangular garden ABCD is 168 metre2 and the perimeter of the grassy area is 60 metre. The pond with uniform depth contains 15.4 metre3 of water.
It is given that DC = 6y metre and BC = 7x metre, x ≠ y. The area of the rectangular garden ABCD is 168 metre2 and the perimeter of the grassy area is 60 metre. The pond with uniform depth contains 15.4 metre3 of water.By using , find the depth, in metre, of water in the pond.
Solution: