SPM Additional Mathematics 2018, Paper 2 (Question 5 & 6)

Question 5 (7 marks):
Mathematics Society of SMK Mulia organized a competition to design a logo for the society.


Diagram 3 shows the circular logo designed by Adrian. The three blue coloured regions are congruent. It is given that the perimeter of the blue coloured region is 20π cm.
[Use π = 3.142]
Find
(a) the radius, in cm, of the logo to the nearest integer,
(b) the area, in cm², of the yellow coloured region.


Solution:
(a)
$\begin{array}{l}6\text{ arcs }=20\pi \\ 6r\theta =20\pi \\ 6r\left[\cancel{{60}^o}\times \frac{\pi }{{\cancel{{180}^o}}^3}\right]=20\pi \\ 2\pi r=20\pi \\ r=10\text{ cm}\end{array}$

(b)

$\begin{array}{l}\text{Area of yellow coloured region}\\ =3\left[\text{area of triangle }OAB\right]-6\left[\text{area of segment}\right]\\ =3\left[\frac{1}{2}ab\sin C\right]-6\left[\frac{1}{2}{r}^2\left(\theta -\sin \theta \right)\right]\\ =3\left[\frac{1}{2}\left(10\right)\left(10\right)\sin {120}^o\right]-6\left[\frac{1}{2}{\left(10\right)}^2\left(\theta -\sin \theta \right)\right]\\ =3\left(43.3013\right)-6\left[50\left(1.0473-\sin 1.0473\right)\right]\leftarrow \boxed{\begin{array}{l}\text{change to rad mode}\\ \theta ={60}^o\times \frac{3.142}{{180}^o}=1.0473\end{array}}\\ =129.9039-6\left(9.0612\right)\\ =129.9039-54.3672\\ =75.54{\text{ cm}}^2\end{array}$

Question 6 (6 marks):
Diagram 4 shows the front view of a part of a roller coaster track in a miniature park.

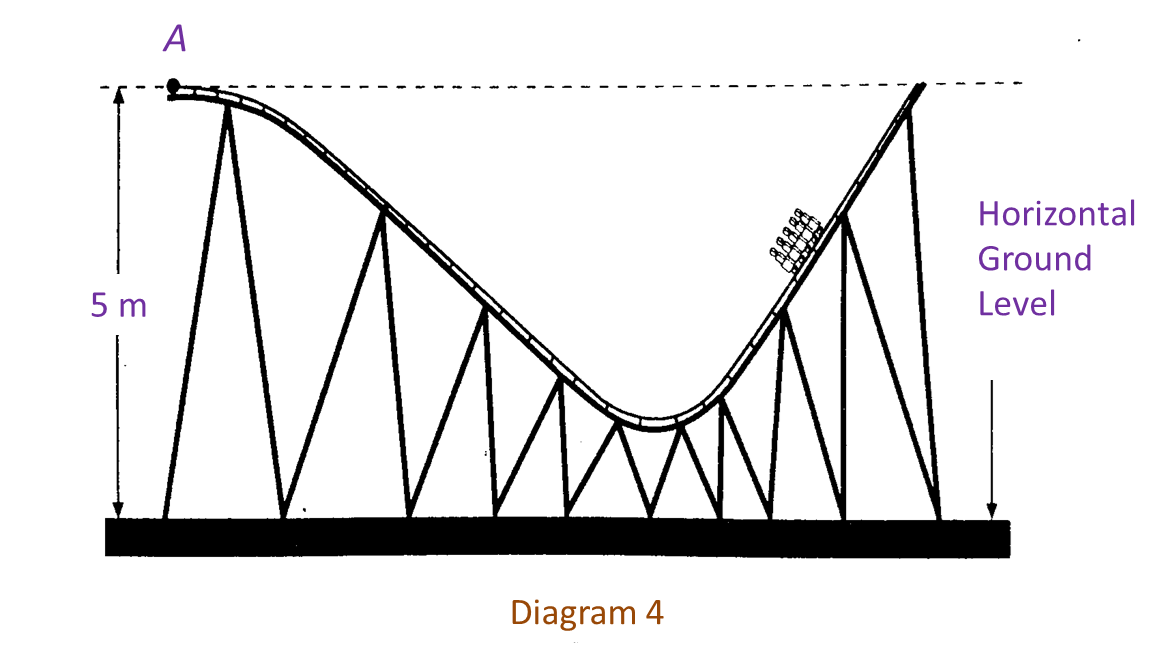
The curve part of the track of the roller coaster is represented by an equation $y=\frac{1}{64}{x}^3-\frac{3}{16}{x}^2$ , with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.


Solution:
$\begin{array}{l}y=\frac{1}{64}{x}^3-\frac{3}{16}{x}^2\mathrm{\dots \dots \dots \dots \dots }\left(1\right)\\ \frac{dy}{dx}=3\left(\frac{1}{64}\right)x^2-2\left(\frac{3}{16}\right)x^1\\ =\frac{3}{64}{x}^2-\frac{3}{8}x\\ \\ \text{At turning point, }\frac{dy}{dx}=0\\ \frac{3}{64}{x}^2-\frac{3}{8}x=0\\ x\left(\frac{3}{64}x-\frac{3}{8}\right)=0\\ x=0\text{ or}\\ \frac{3}{64}x-\frac{3}{8}=0\\ \frac{3}{64}x=\frac{3}{8}\\ x=\frac{3}{8}\times \frac{64}{3}\\ x=8\\ \\ \text{Substitute values of }x\text{ into equation (1):}\\ \text{When }x=0,\\ y=\frac{1}{64}{\left(0\right)}^3-\frac{3}{16}{\left(0\right)}^2\\ y=0\\ \\ \text{When }x=8,\\ y=\frac{1}{64}{\left(8\right)}^3-\frac{3}{16}{\left(8\right)}^2\\ y=-4\\ \\ \text{Thus, turning points : }\left(0,\text{ 0}\right)\text{ and }\left(8,-4\right)\end{array}$

$\begin{array}{l}\frac{dy}{dx}=\frac{3}{64}{x}^2-\frac{3}{8}x\\ \frac{d^{2}y}{d{x}^2}=2\left(\frac{3}{64}\right)x-\frac{3}{8}\\ =\frac{3}{32}x-\frac{3}{8}\\ \\ \text{When }x=0,\\ \frac{d^{2}y}{d{x}^2}=\frac{3}{32}\left(0\right)-\frac{3}{8}\\ =-\frac{3}{8}\left(<0\right)\\ \left(0,0\right)\text{ is maximum point}\text{.}\\ \\ \text{When }x=8,\\ \frac{d^{2}y}{d{x}^2}=\frac{3}{32}\left(8\right)-\frac{3}{8}\\ =\frac{3}{8}\left(>0\right)\\ \left(8,-4\right)\text{ is minimum point}\text{.}\\ \\ \text{Shortest vertical distance between track }\\ \text{and ground level is at the minimum point}\text{.}\\ \text{Shortest vertical distance}\\ =5-4\\ =1\text{ m}\end{array}$