SPM Additional Mathematics 2018, Paper 2 (Question 7 – 9)

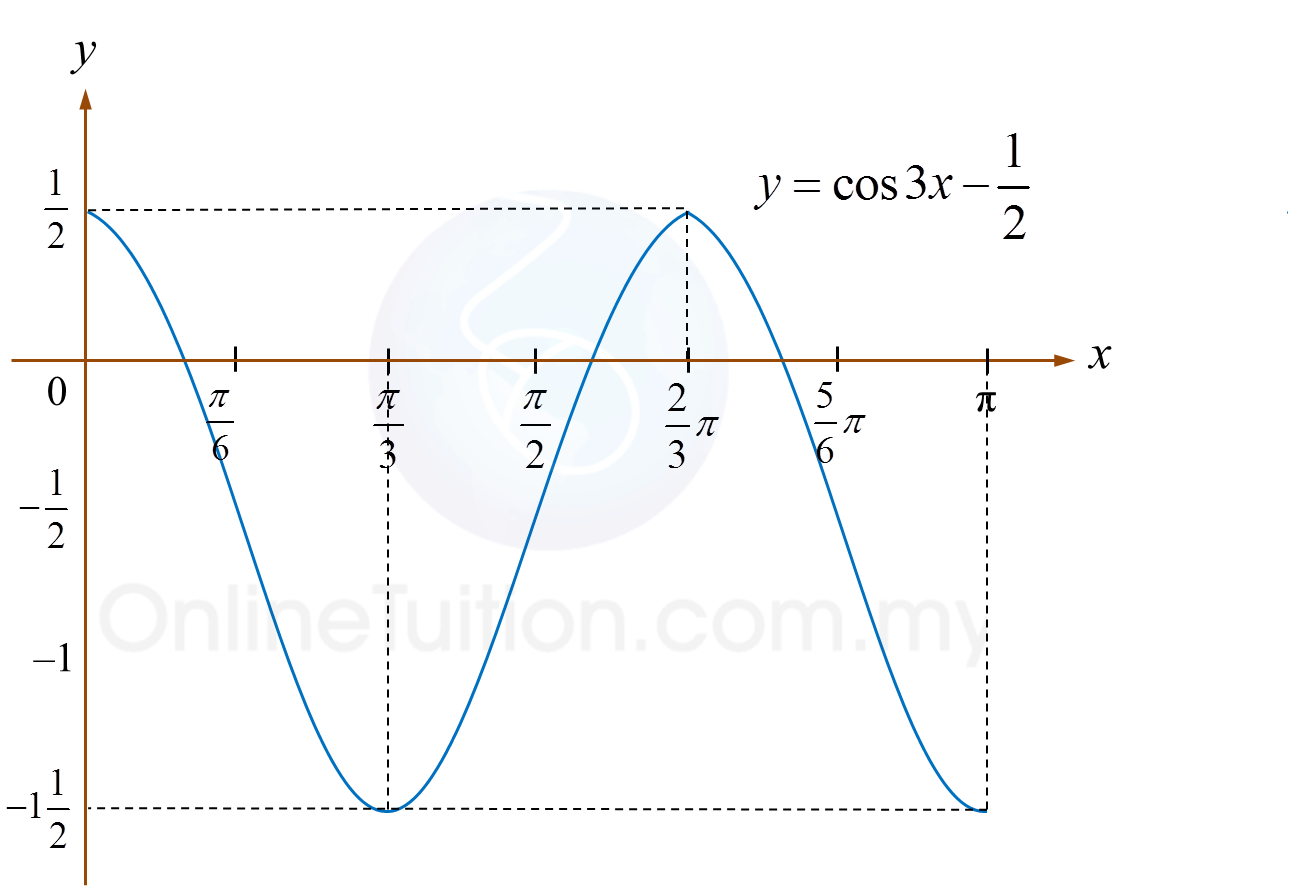
Question 7 (10 marks):
$\begin{array}{l}\left(a\right)\text{ Prove }\sin \left(3x+\frac{\pi }{6}\right)-\sin \left(3x-\frac{\pi }{6}\right)=\cos 3x\\ \left(b\right)\text{ Hence,}\\ \left(i\right)\text{ solve the equation s}in\left(\frac{3x}{2}+\frac{\pi }{6}\right)-\sin \left(\frac{3x}{2}-\frac{\pi }{6}\right)=\frac{1}{2}\text{ for }0\le x\le 2\pi \\ \text{ and give your answer in the simplest fraction form in terms of }\pi \text{ radian}\text{.}\\ \left(ii\right)\text{ sketch the graph of }y=\text{s}in\left(3x+\frac{\pi }{6}\right)-\sin \left(3x-\frac{\pi }{6}\right)-\frac{1}{2}\text{ for }0\le x\le \pi .\end{array}$


Solution:
$\begin{array}{l}\left(a\right)\text{ Left hand side},\\ \sin \left(3x+\frac{\pi }{6}\right)-\sin \left(3x-\frac{\pi }{6}\right)\\ =\left[\sin 3x\cos \frac{\pi }{6}+\cos 3x\sin \frac{\pi }{6}\right]-\left[\sin 3x\cos \frac{\pi }{6}-\cos 3x\sin \frac{\pi }{6}\right]\\ =2\left[\cos 3x\sin \frac{\pi }{6}\right]\\ =2\left[\cos 3x\left(\frac{1}{2}\right)\right]\\ =\cos 3x\left(\text{right hand side}\right)\end{array}$

$\begin{array}{l}\left(b\right)\left(i\right)\\ \sin \left(\frac{3x}{2}+\frac{\pi }{6}\right)-\sin \left(\frac{3x}{2}-\frac{\pi }{6}\right)=\frac{1}{2},0\le x\le 2\pi \\ \cos \frac{3x}{2}=\frac{1}{2}\\ \frac{3x}{2}=\frac{\pi }{3},\left(2\pi -\frac{\pi }{3}\right),\left(2\pi +\frac{\pi }{3}\right)\\ \frac{3x}{2}=\frac{\pi }{3},\frac{5\pi }{3},\frac{7\pi }{3}\\ x=\frac{2\pi }{9},\frac{10\pi }{9},\frac{14\pi }{9}\end{array}$


$\begin{array}{l}\left(b\right)\left(ii\right)\\ y=\text{s}in\left(3x+\frac{\pi }{6}\right)-\sin \left(3x-\frac{\pi }{6}\right)-\frac{1}{2}\text{ for }0\le x\le \pi .\\ y=\cos 3x-\frac{1}{2}\end{array}$

Question 8 (10 marks):
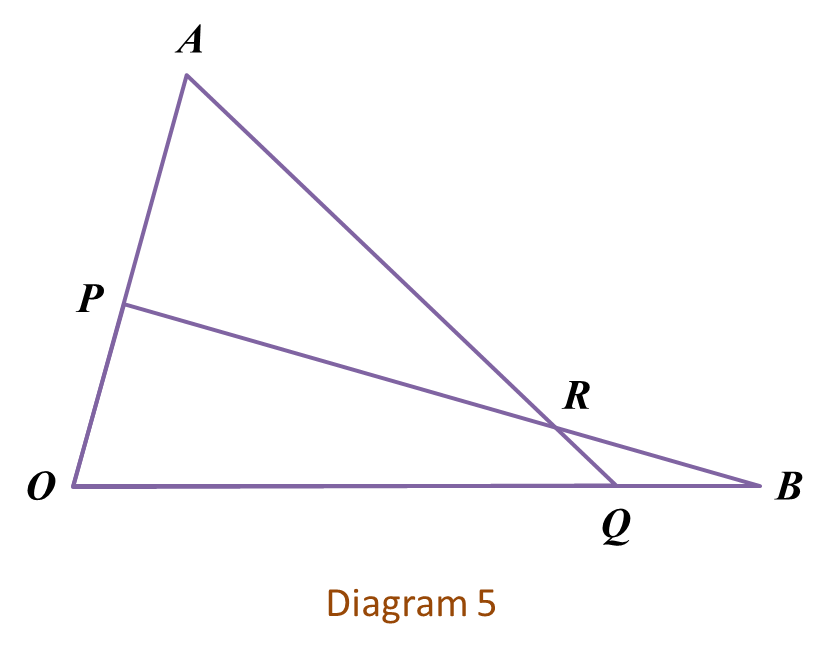
Diagram 5 shows triangles OAQ and OPB where point P lies on OA and point Q lies on OB. The straight lines AQ and PB intersect at point R.
$\begin{array}{l}\text{It is given that }\overrightarrow{OA}=18\underset{˜}{x},\overrightarrow{OB}=16\underset{˜}{y},OP:PA=1:2,OQ:QB=3:1,\\ \overrightarrow{PR}=m\overrightarrow{PB}\text{ and }\overrightarrow{QR}=n\overrightarrow{QA},\text{ where }m\text{ and }n\text{ are constants}\text{.}\\ \left(a\right)\text{ Express }\overrightarrow{OR}\text{ in terms of}\\ \left(i\right)m,\underset{˜}{x}\text{ and }\underset{˜}{y},\\ \left(ii\right)n,\underset{˜}{x}\text{ and }\underset{˜}{y},\\ \left(b\right)\text{ Hence, find the value of }m\text{ and of }n.\\ \left(c\right)\text{ Given }\left|\underset{˜}{x}\right|=2\text{ units, }\left|\underset{˜}{y}\right|=1\text{ unit and }OA\text{ is perpendicular to }OB\text{ calculate }\left|\overrightarrow{PR}\right|.\end{array}$


Solution: 
(a)(i)
$\begin{array}{l}\overrightarrow{OR}=\overrightarrow{OP}+\overrightarrow{PR}\\ =\frac{1}{3}\overrightarrow{OA}+m\overrightarrow{PB}\\ =\frac{1}{3}\left(18\underset{˜}{x}\right)+m\left(\overrightarrow{PO}+\overrightarrow{OB}\right)\\ =6\underset{˜}{x}+m\left(-6\underset{˜}{x}+16\underset{˜}{y}\right)\end{array}$

(a)(ii)
$\begin{array}{l}\overrightarrow{OR}=\overrightarrow{OQ}+\overrightarrow{QR}\\ =\frac{3}{4}\overrightarrow{OB}+n\overrightarrow{QA}\\ =\frac{3}{4}\left(16\underset{˜}{y}\right)+n\left(\overrightarrow{QO}+\overrightarrow{OA}\right)\\ =12\underset{˜}{y}+n\left(-12\underset{˜}{y}+18\underset{˜}{x}\right)\\ =\left(12-12n\right)\underset{˜}{y}+18n\underset{˜}{x}\end{array}$



(b)
$\begin{array}{l}6\underset{˜}{x}+m\left(-6\underset{˜}{x}+16\underset{˜}{y}\right)=\left(12-12n\right)\underset{˜}{y}+18n\underset{˜}{x}\\ 6\underset{˜}{x}-6m\underset{˜}{x}+16m\underset{˜}{y}=18n\underset{˜}{x}+12\underset{˜}{y}-12n\underset{˜}{y}\\ \text{by comparison;}\\ 6-6m=18n\\ 1-m=3n\\ m=1-3n\mathrm{\dots \dots \dots \dots ..}\left(1\right)\\ \\ 16m=12-12n\\ 4m=3-3n\mathrm{\dots \dots \dots \dots ..}\left(2\right)\\ \\ \text{Substitute (1) into (2),}\\ 4\left(1-3n\right)=3-3n\\ 4-12n=3-3n\\ 9n=1\\ n=\frac{1}{9}\\ \\ \text{Substitute }n=\frac{1}{9}\text{ into (1),}\\ m=1-3\left(\frac{1}{9}\right)\\ m=\frac{2}{3}\end{array}$



(c)
$\begin{array}{l}\left|\underset{˜}{x}\right|=2\text{, }\left|\underset{˜}{y}\right|=1\\ \overrightarrow{PR}=\frac{2}{3}\overrightarrow{PB}\\ =\frac{2}{3}\left(-6\underset{˜}{x}+16\underset{˜}{y}\right)\\ =-4\underset{˜}{x}+\frac{32}{3}\underset{˜}{y}\\ \\ \left|\overrightarrow{PR}\right|=\sqrt{{\left[-4\left(2\right)\right]}^2+{\left[\frac{32}{3}\left(1\right)\right]}^2}\\ =\sqrt{\frac{1600}{9}}\\ =\frac{40}{3}\text{ units}\end{array}$

Question 9 (10 marks):
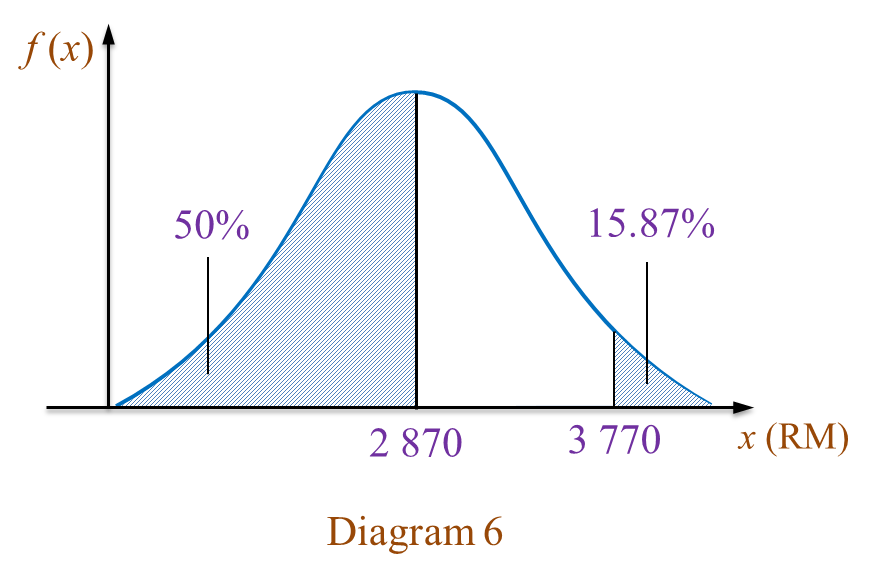
A study shows that the credit card balance of the customers is normally distributed as shown in Diagram 6.

(a)(i) Find the standard deviation.
(ii) If 30 customers are chosen at random, find the number of customers who have a credit card balance between RM1800 and RM3000.
(b) It is found that 25% of the customers have a credit card balance less than RM y.
Find the value of y.


Solution:
(a)(i)
$\begin{array}{l}\mu =2870,x=3770\\ P\left(X>3770\right)=15.87\%\\ P\left(Z>\frac{3770-2870}{\sigma }\right)=0.1587\\ P\left(Z>1.0\right)=0.1587\\ \frac{3770-2870}{\sigma }=1.0\\ \sigma =900\end{array}$


(a)(ii)
$\begin{array}{l}P\left(1800<X<3000\right)\\ =P\left(\frac{1800-2870}{900}<Z<\frac{3000-2870}{900}\right)\\ =P\left(-1.189<Z<0.144\right)\\ =1-P\left(Z\le -1.189\right)-P\left(Z\ge 0.144\right)\\ =1-0.1172-0.4427\\ =0.4401\\ \\ \text{Number of customers}=0.4401\times 30\\ =14\end{array}$


(b)
$\begin{array}{l}\mu =2870,x=y\\ P\left(x<y\right)=25\%\\ P\left(Z<\frac{y-2870}{900}\right)=0.25\\ \frac{y-2870}{900}=-0.674\\ y=2263.40\end{array}$