\

2.13.6 Quadratic Functions, SPM Practice (Long Questions)


Question 11:


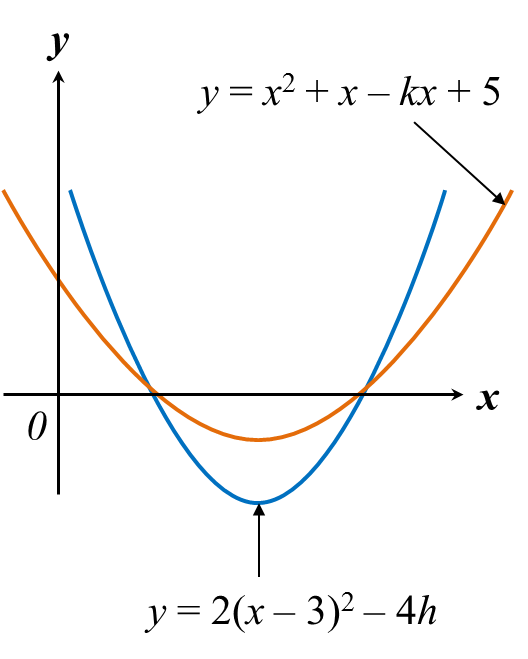
Diagram above shows the graphs of the curves y = x2 + x – kx + 5 and y = 2(x – 3) – 4h that intersect the x-axis at two points. Find
(a) the value of k and of h,
(b) the minimum value of each curve.


Solution:
(a)
y= x 2 +x−kx+5 = x 2 +( 1−k )x+5 = [ x+ ( 1−k ) 2 ] 2 − ( 1−k 2 ) 2 +5 axis of symmetry of the graph is x=− ( 1−k ) 2

y=2 ( x−3 ) 2 −4h axis of symmetry of the graph is x=3. ∴ − 1−k 2 =3 −1+k=6 k=7

Substitute k=7 into equation y= x 2 +x−7x+5   = x 2 −6x+5 At x-axis,y=0; x 2 −6x+5=0 ( x−1 )( x−5 )=0 x=1,5

At point ( 1,0 ) Substitute x=1,y=0 into the graph: y=2 ( x−3 ) 2 −4h 0=2 ( 1−3 ) 2 −4h 4h=2( 4 ) 4h=8 h=2

(b)
For y= x 2 −6x+5 = ( x−3 ) 2 −9+5 = ( x−3 ) 2 −4 ∴ Minimum value is −4. For y=2 ( x−3 ) 2 −8, minimum value is−8.

Question 12:
Quadratic function f(x) = x2 – 4px + 5p2 + 1 has a minimum value of m2 + 2p, where m and p are constants.
(a) By using the method of completing the square, shows that m = p – 1.
(b) Hence, find the values of p and of m if the graph of the quadratic function is symmetry at x = m2 – 1.

Solution:
(a)
f( x )= x 2 −4px+5 p 2 +1 = x 2 −4px+ ( −4p 2 ) 2 − ( −4p 2 ) 2 +5 p 2 +1 = ( x−2p ) 2 + p 2 +1 Minimum value, m 2 +2p= p 2 +1 m 2 = p 2 −2p+1 m 2 = ( p−1 ) 2 m=p−1

(b)
x= m 2 −1 2p= m 2 −1 p= m 2 −1 2 Given m=p−1⇒p=m+1 m+1= m 2 −1 2 2m+2= m 2 −1 m 2 −2m−3=0 ( m−3 )( m+1 )=0 m=3 or −1 When m=3, p= 3 2 −1 2 =4 When m=−1, p= ( −1 ) 2 −1 2 =0

Leave a Comment