Question 11:
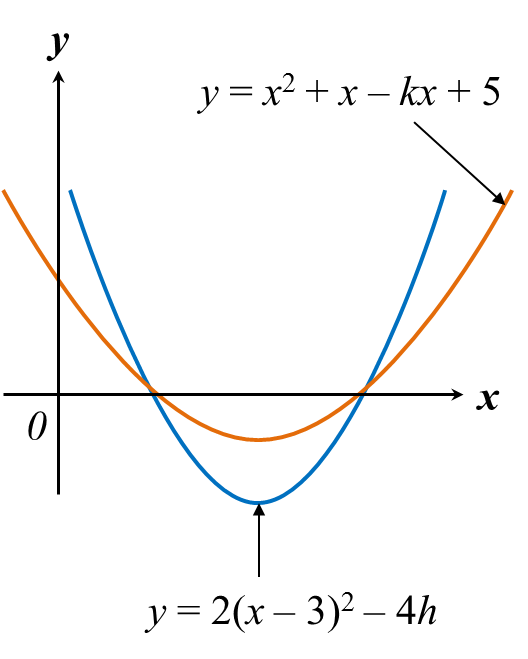
Diagram above shows the graphs of the curves y = x2 + x – kx + 5 and y = 2(x – 3) – 4h that intersect the x-axis at two points. Find
(a) the value of k and of h,
(b) the minimum value of each curve.
Solution:
(a)
y=x2+x−kx+5=x2+(1−k)x+5=[x+(1−k)2]2−(1−k2)2+5axis of symmetry of the graph isx=−(1−k)2
y=2(x−3)2−4haxis of symmetry of the graph is x=3.∴ −1−k2=3−1+k=6k=7
Substitute k=7 into equationy=x2+x−7x+5 =x2−6x+5At x-axis,y=0;x2−6x+5=0(x−1)(x−5)=0x=1,5
At point (1,0)Substitute x=1,y=0 into the graph:y=2(x−3)2−4h0=2(1−3)2−4h4h=2(4)4h=8h=2
(b)
For y=x2−6x+5=(x−3)2−9+5=(x−3)2−4∴ Minimum value is −4.For y=2(x−3)2−8, minimum value is−8.
Diagram above shows the graphs of the curves y = x2 + x – kx + 5 and y = 2(x – 3) – 4h that intersect the x-axis at two points. Find
(a) the value of k and of h,
(b) the minimum value of each curve.
Solution:
(a)
y=x2+x−kx+5=x2+(1−k)x+5=[x+(1−k)2]2−(1−k2)2+5axis of symmetry of the graph isx=−(1−k)2
y=2(x−3)2−4haxis of symmetry of the graph is x=3.∴ −1−k2=3−1+k=6k=7
Substitute k=7 into equationy=x2+x−7x+5 =x2−6x+5At x-axis,y=0;x2−6x+5=0(x−1)(x−5)=0x=1,5
At point (1,0)Substitute x=1,y=0 into the graph:y=2(x−3)2−4h0=2(1−3)2−4h4h=2(4)4h=8h=2
(b)
For y=x2−6x+5=(x−3)2−9+5=(x−3)2−4∴ Minimum value is −4.For y=2(x−3)2−8, minimum value is−8.
Question 12:
Quadratic function f(x) = x2 – 4px + 5p2 + 1 has a minimum value of m2 + 2p, where m and p are constants.
(a) By using the method of completing the square, shows that m = p – 1.
(b) Hence, find the values of p and of m if the graph of the quadratic function is symmetry at x = m2 – 1.
Solution:
(a)
f(x)=x2−4px+5p2+1=x2−4px+(−4p2)2−(−4p2)2+5p2+1=(x−2p)2+p2+1Minimum value,m2+2p=p2+1m2=p2−2p+1m2=(p−1)2m=p−1
(b)
x=m2−12p=m2−1p=m2−12Given m=p−1⇒p=m+1m+1=m2−122m+2=m2−1m2−2m−3=0(m−3)(m+1)=0m=3 or −1When m=3,p=32−12=4When m=−1,p=(−1)2−12=0
Quadratic function f(x) = x2 – 4px + 5p2 + 1 has a minimum value of m2 + 2p, where m and p are constants.
(a) By using the method of completing the square, shows that m = p – 1.
(b) Hence, find the values of p and of m if the graph of the quadratic function is symmetry at x = m2 – 1.
Solution:
(a)
f(x)=x2−4px+5p2+1=x2−4px+(−4p2)2−(−4p2)2+5p2+1=(x−2p)2+p2+1Minimum value,m2+2p=p2+1m2=p2−2p+1m2=(p−1)2m=p−1
(b)
x=m2−12p=m2−1p=m2−12Given m=p−1⇒p=m+1m+1=m2−122m+2=m2−1m2−2m−3=0(m−3)(m+1)=0m=3 or −1When m=3,p=32−12=4When m=−1,p=(−1)2−12=0