1.5.1 Circular Measure SPM Practice (Paper 2 Question 1 - 5)

Question 1:

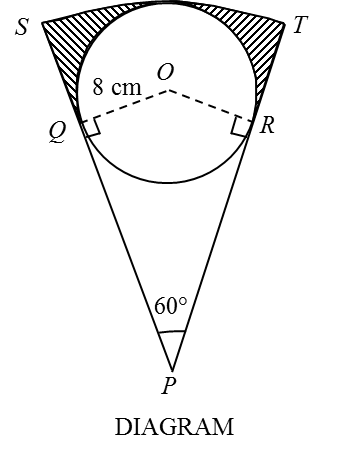
Diagram shows a circle, centre O and radius 8 cm inscribed in a sector SPT of a circle at centre P. The straight lines, SP and TP, are tangents to the circle at point Q and point R, respectively.

[Use p= 3.142]

Calculate

(a) the length, in cm, of the arc ST,

(b) the area, in cm², of the shaded region.

Solution:
(a)

\begin{array}{l} For triangle O P Q \\ \sin 30^{\circ} = \frac{8}{O P} \\ O P = \frac{8}{\sin 30^{\circ}} = 16 cm \\ Radius of sector S P T = 16 + 8 = 24 cm \\ ∠ S P T = 60 \times \frac{3.142}{180} = 1.047 radian \\ Length of arc S T = 24 \times 1.047 = 25.14 cm \end{array}

(b)

\begin{array}{l} For triangle O P Q : \\ \tan 30^{\circ} = \frac{8}{Q P} \\ P Q = \frac{8}{\tan 30^{\circ}} = 13.86 cm \\ ∠ Q O R = 2 (60^{\circ}) = 120^{\circ} \\ Reflex angle ∠ Q O R = 360^{\circ} - 120^{\circ} = 240^{\circ} \\ 240^{\circ} = \frac{3.142}{180^{\circ}} \times 240^{\circ} = 4.189 radian \\ Area of shaded region \\ = (\begin{array}{l} Area of \\ sector S P T \end{array}) - (\begin{array}{l} Area of major \\ sector O Q R \end{array}) - (\begin{array}{l} Area of triangle \\ O P Q and O P R \end{array}) \\ = \frac{1}{2} {(24)}^{2} (1.047) - \frac{1}{2} {(8)}^{2} (4.189) - 2 (\frac{1}{2} \times 8 \times 13.86) \\ = 301.54 - 134.05 - 110.88 \\ = 56.61 {cm}^{2} \end{array}

Question 2:
Diagram below shows a semicircle PTQ, with centre O and quadrant of a circle RST, with centre R.

[Use π = 3.142]
Calculate
(a) the value of θ, in radians,
(b) the perimeter, in cm, of the whole diagram,
(c) the area, in cm², of the shaded region.

Solution:

\begin{array}{l} (a) \\ \sin ∠ R O T = \frac{2.5}{5} \\ ∠ R O T = 30^{o} \\ θ = 180^{o} - 30^{o} = 150^{o} \\ = 150 \times \frac{π}{180} \\ = 2.618 rad \end{array}

\begin{array}{l} (b) \\ Length of arc P T = r θ \\ = 5 \times 2.618 \\ = 13.09 cm \\ Length of arc S T = \frac{π}{2} \times 2.5 \\ = 3.9275 cm \\ O R^{2} + {2.5}^{2} = 5^{2} \\ O R^{2} = 5^{2} - {2.5}^{2} \\ O R = 4.330 \\ Perimeter = 13.09 + 3.9275 + 2.5 + 4.330 + 5 \\ = 28.8475 cm \end{array}

\begin{array}{l} (c) \\ Area of shaded region \\ = Area of quadrant R S T - Area of quadrant R Q T \\ Area of quadrant R Q T \\ = Area of O Q T - Area of O T R \\ = \frac{1}{2} {(5)}^{2} \times (30 \times \frac{π}{180}) - \frac{1}{2} (4.33) (2.5) \\ = 1.1333 {cm}^{2} \\ Area of shaded region \\ = Area of quadrant R S T - Area of quadrant R Q T \\ = \frac{1}{2} {(2.5)}^{2} \times (90 \times \frac{π}{180}) - 1.1333 \\ = 3.7661 {cm}^{2} \end{array}

Question 3:

Diagram below shows two circles. The larger circle has centre A and radius 20 cm. The smaller circle has centre B and radius 12 cm. The circles touch at point R. The straight line PQ is a common tangent to the circles at point P and point Q.

[Use π = 3.142]

Given that angle PAR = θ radians,

(a) show that θ = 1.32 ( to two decimal places),

(b) calculate the length, in cm, of the minor arc QR,

(c) calculate the area, in cm², of the shaded region.

Solution:
(a)

\begin{array}{l} In △ B S A \\ \cos θ = \frac{8}{32} = \frac{1}{4} \\ θ = 1.32 rad (2 d .p .) \end{array}

(b)

Angle QBR = 3.142 – 1.32 = 1.822 rad

Length of minor arc QR

= 12 × 1.822

= 21.86 cm

(c)

P Q = \sqrt{32^{2} - 8^{2}} = 30.98 cm

Area of the shaded region

= Area of trapezium PQBA– Area of sector QBR – Area of sector PAR

= ½ (12 + 20) (30.98) – ½ (12)² (1.822) – ½ (20)²(1.32)

= 495.68 – 131.18 – 264

= 100.5 cm²

Question 4:
Diagram below shows a sector QPR with centre P and sector POQ, with centre O.

It is given that OP = 17 cm and PQ = 8.8 cm.
[Use π = 3.142]
Calculate
(a) angle OPQ, in radians,
(b) the perimeter, in cm, of sector QPR,
(c) the area, in cm², of the shaded region.

Solution:

\begin{array}{l} (a) \\ ∠ O P Q = ∠ O Q P \\ x + x + 30 = 180 \\ 2 x = 150 \\ x = 75 \\ ∠ O P Q = \frac{75 \times 3.142}{180} \\ = 1.3092 radians \end{array}

\begin{array}{l} (b) \\ Length of arc Q R = r θ \\ = 8.8 \times 1.3092 \\ = 11.52 cm \\ Perimeter of sector Q P R \\ = 11.52 + 8.8 + 8.8 \\ = 29.12 cm \end{array}

\begin{array}{l} (c) \\ 30^{o} = \frac{30 \times 3.142}{180} = 0.5237 rad \\ Area of segment P Q \\ = \frac{1}{2} r^{2} (θ - \sin θ) \\ = \frac{1}{2} \times 17^{2} \times (0.5237 - \sin 30) \\ = \frac{1}{2} \times 289 \times (0.5237 - 0.5) \\ = 3.4247 {cm}^{2} \\ Area of sector Q P R \\ = \frac{1}{2} r^{2} θ \\ = \frac{1}{2} \times {8.8}^{2} \times 1.3092 \\ = 50.692 {cm}^{2} \\ Area of shaded region \\ = 3.4247 + 50.692 \\ = 54.1167 {cm}^{2} \end{array}

Question 5:

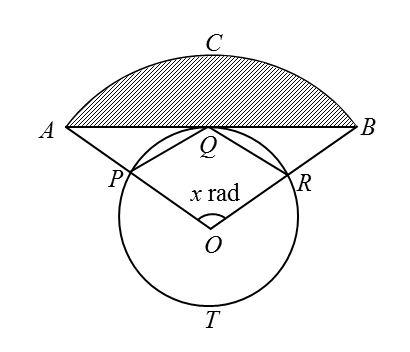
Diagram below shows a circle PQRT, centre O and radius 5 cm. AQB is a tangent to the circle at Q. The straight lines, AO and BO, intersect the circle at P and R respectively.

OPQR is a rhombus. ACB is an arc of a circle at centre O.

Calculate

(a) the angle x , in terms of π ,

(b) the length , in cm , of the arc ACB ,

(c) the area, in cm²,of the shaded region.

Solution:

(a)

Rhombus has 4 equal sides, therefore OP = PQ = QR = OR = 5 cm

OR is radius to the circle, therefore OR = OQ = 5 cm

Triangles OQR and OQP are equilateral triangle,

Therefore, ∠ QOR= ∠QOP = 60^o

∠ POR = 120^o

x = 120^o × π/180^o

x = 2π/ 3 rad

(b)

cos ∠ AOQ= OQ / OA

cos 60^o = 5 / OA

OA = 10 cm

Length of arc, ACB,

s = r θ

Arc ACB = (10) (2π / 3)

Arc ACB = 20.94 cm

(c)

\begin{array}{l} Area of shaded region \\ = \frac{1}{2} r^{2} (θ - \sin θ) (change calculator to Rad mode) \\ = \frac{1}{2} {(10)}^{2} (\frac{2 π}{3} - \sin \frac{2 π}{3}) \\ = 50 (2.094 - 0.866) \\ = 61.40 {cm}^{2} \end{array}

1.5.1 Circular Measure SPM Practice (Paper 2 Question 1 – 5)

1 thought on “1.5.1 Circular Measure SPM Practice (Paper 2 Question 1 – 5)”

Leave a Comment Cancel reply