Question 11 (SPM 2019):
Diagram 4 shows a rhombus OACB inscribed in sector AOB with centre O and radius r cm.
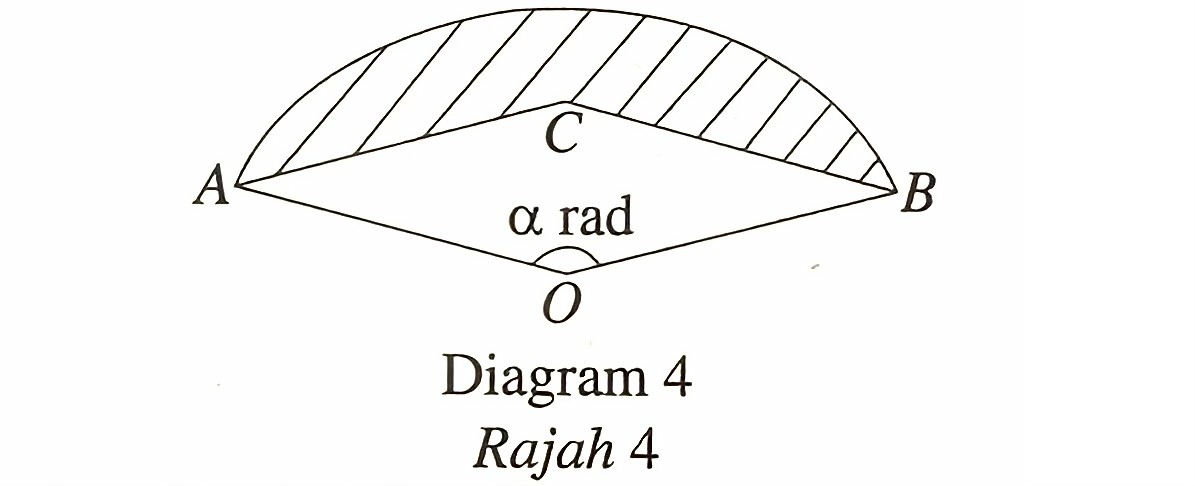
Given the area of sector AOB is 18 cm2, express
(a) α in terms of r,
(b) the perimeter, in cm, of the shaded region in terms of r.
[3 marks]
Answer:
(a)
$$ \begin{aligned} &\text { Area of sector } A O B=18 \mathrm{~cm}^2\\ &\begin{aligned} & \frac{1}{2} r^2 \alpha=18 \\ & \alpha=\frac{36}{r^2} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Length of } \operatorname{arc} A B=r \alpha\\ &=r\left(\frac{36}{r^2}\right)=\frac{36}{r} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter of shaded region }\\ &\begin{aligned} & =\frac{36}{r}+A C+C B \\ & =\frac{36}{r}+r+r=\frac{36}{r}+2 r \end{aligned} \end{aligned} $$
Diagram 4 shows a rhombus OACB inscribed in sector AOB with centre O and radius r cm.

Given the area of sector AOB is 18 cm2, express
(a) α in terms of r,
(b) the perimeter, in cm, of the shaded region in terms of r.
[3 marks]
Answer:
(a)
$$ \begin{aligned} &\text { Area of sector } A O B=18 \mathrm{~cm}^2\\ &\begin{aligned} & \frac{1}{2} r^2 \alpha=18 \\ & \alpha=\frac{36}{r^2} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Length of } \operatorname{arc} A B=r \alpha\\ &=r\left(\frac{36}{r^2}\right)=\frac{36}{r} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter of shaded region }\\ &\begin{aligned} & =\frac{36}{r}+A C+C B \\ & =\frac{36}{r}+r+r=\frac{36}{r}+2 r \end{aligned} \end{aligned} $$