Question 1:
(a)
(b)

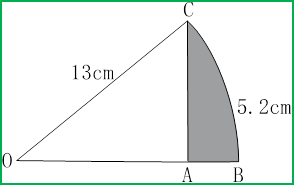
The figure shows the sector OCB of radius 13 cm at the centre O. The length of the arc CB = 5.2 cm. Find
(a) the angle in radians,
(b) the perimeter of the shaded region.
Solution:(a)
(b)
Perimeter of the shaded region = 5.07 + 1.03 + 5.2 = 11.3 cm.
Question 2:
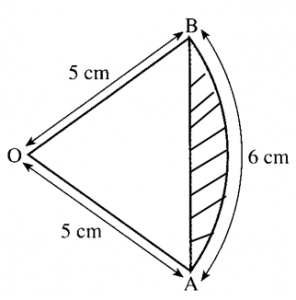
The figure shows the sector AOB of a circle, centre O and radius 5 cm. The length of the arc AB is 6 cm. Find the area of:
Solution:
(a) Arc AB = 6cm

The figure shows the sector AOB of a circle, centre O and radius 5 cm. The length of the arc AB is 6 cm. Find the area of:
(a) the sector AOB,
(b) the shaded region.
(a) Arc AB = 6cm
s = r θ
6 = 5 θ
θ = 6/5 rad
(b)
Question 3:
Solution:
Diagram below shows a sector QOR of a circle with centre O.
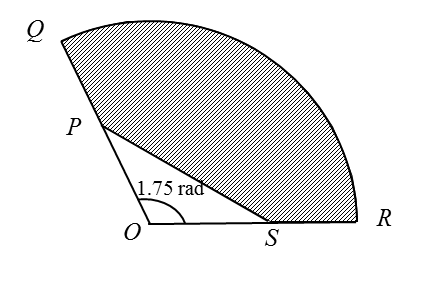

It is given that PS = 8 cm and QP = PO= OS = SR = 5 cm.
Find
(a) the length, in cm, of the arc QR,
(b) the area, in cm2, of the shaded region.
(a) Length of arc QR = r θ = 10 (1.75) = 17.5 cm
(b)
Area of the shaded region
= Area of sector QOR – Area of triangle POS
= ½ (10)2 (1.75) – ½ (5) (5) sin 1.75 (change calculator to Rad mode)
= 87.5 – 12.30
= 75.2 cm2
Question 4:
Solution:
Diagram below shows a circle with centre O.

The length of the minor arc is 16 cm and the angle of the major sector AOB is 290o.
Using π = 3.142, find
(a) the value of θ, in radians. (Give your answer correct to four significant figures)
(b) the length, in cm, of the radius of the circle.
(a)
Angle of the minor sector AOB
= 360o – 290o
= 70o
= 70o ×
= 1.222 radians
(b)
Using s = rθ
r × 1.222 = 16
radius, r = 13.09 cm
Question 5:
Solution:
(a) s = r θ
Diagram below shows sector OPQ with centre O and sector PXY with centre P.
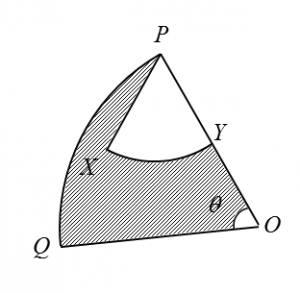 Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,
Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,
 Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,
Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,calculate
( a) the value of θ , in radian ,
( b) the area, in cm2 , of the shaded region .
(a) s = r θ
6 = 8 θ
θ = 0.75 rad
(b)
Area of the shaded region
= Area of sector OPQ – Area of sector PXY
= 24 – 5.4
= 18.6 cm2
Question 6:
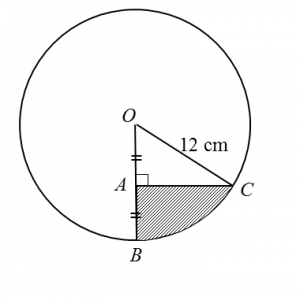 Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find
Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find
Solution:
Diagram below shows a circle with centre O and radius 12 cm.
 Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find
Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find(a) ∠BOC, in radians,
(b) the area, in cm2, of the shaded region.
(a) For triangle OAC,
cos ∠AOC = 6/12
ÐAOC = 1.047 rad (change calculator to Rad mode)
ÐBOC = 1.047 rad
(b)
Area of the shaded region
= Area of BOC – Area of triangle AOC
= ½ (12)2 (1.047) – ½ (6) (12) sin 1.047 (change calculator to Rad mode)
= 75.38 – 31.17
= 44.21 cm2
Question 7 (SPM 2017 – 3 marks):
Diagram 7 shows two sectors AOD and BOC of two concentric circles with centre O.
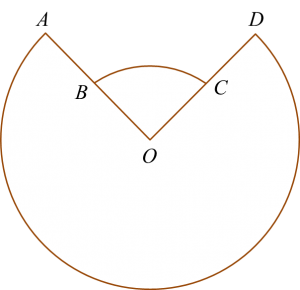 Diagram 7
Diagram 7
The angle subtended at the centre O by the major arc AD is 7α radians and the perimeter of the whole diagram is 50 cm.
Given OB = r cm, OA = 2OB and ∠BOC = 2α, express r in terms of α.
Solution:
Diagram 7 shows two sectors AOD and BOC of two concentric circles with centre O.
 Diagram 7
Diagram 7The angle subtended at the centre O by the major arc AD is 7α radians and the perimeter of the whole diagram is 50 cm.
Given OB = r cm, OA = 2OB and ∠BOC = 2α, express r in terms of α.
Solution:
Question 8 (SPM 2018 – 4 marks):
Diagram 5 shows a circle with centre O.
 Diagram 5
Diagram 5
PR and QR are tangents to the circle at points P and Q respectively. It is given that the length of minor arc PQ is 4 cm and
Express in terms of α,
(a) the radius, r, of the circle,
(b) the area, A, of the shaded region.
Solution:
(a)
(b)
Diagram 5 shows a circle with centre O.
 Diagram 5
Diagram 5PR and QR are tangents to the circle at points P and Q respectively. It is given that the length of minor arc PQ is 4 cm and
Express in terms of α,
(a) the radius, r, of the circle,
(b) the area, A, of the shaded region.
Solution:
(a)
(b)
Question 9 (SPM 2005):
Diagram 6 shows a circle with centre O.
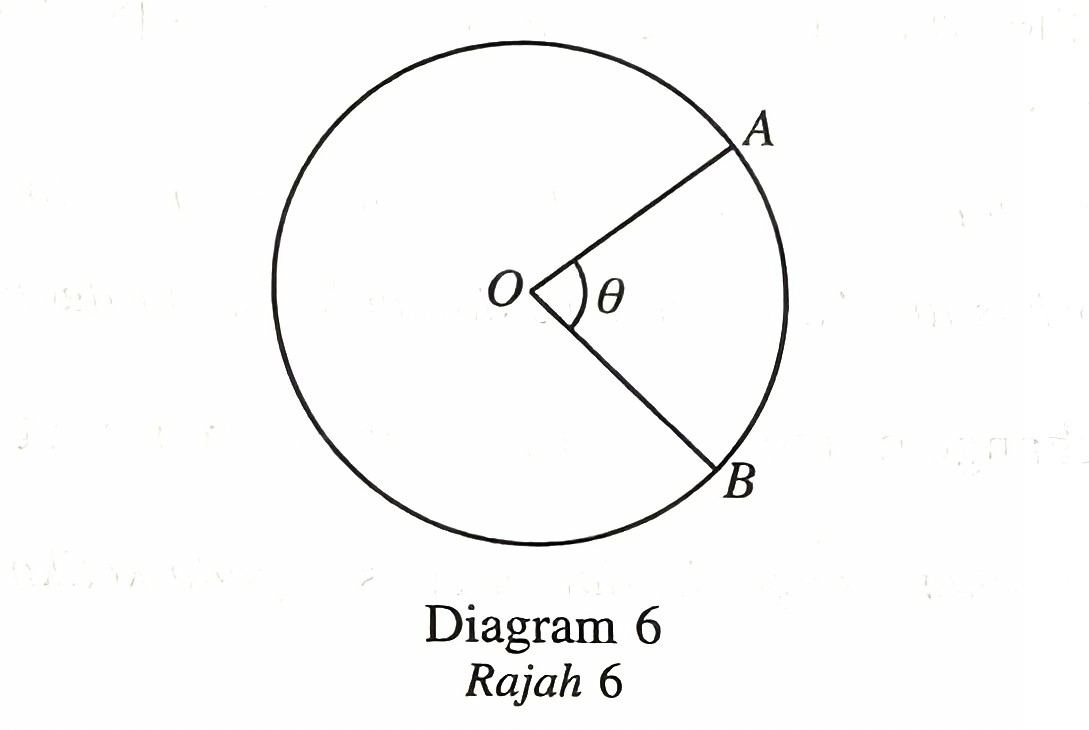 The length of the minor arc AB is 16 cm and the angle of the major sector AOB is 290o.
The length of the minor arc AB is 16 cm and the angle of the major sector AOB is 290o.
Using π = 3.142, find
(a) the value of θ, in radians.
(Give your answer correct to four significant figures.)
(b) the length, in cm , of the radius of the circle.
[3 marks]
Answer:
(a)
$$ \begin{aligned} \theta & =360^{\circ}-290^{\circ} \\ & =70^{\circ} \\ & =70 \times \frac{3.142}{180} \\ & =1.222 \text { radians } \end{aligned} $$
(b)
$$ \begin{aligned} 16 & =r \times 1.222 \\ r & =\frac{16}{1.222} \\ & =13.09 \mathrm{~cm} \end{aligned} $$
Diagram 6 shows a circle with centre O.
 The length of the minor arc AB is 16 cm and the angle of the major sector AOB is 290o.
The length of the minor arc AB is 16 cm and the angle of the major sector AOB is 290o.Using π = 3.142, find
(a) the value of θ, in radians.
(Give your answer correct to four significant figures.)
(b) the length, in cm , of the radius of the circle.
[3 marks]
Answer:
(a)
$$ \begin{aligned} \theta & =360^{\circ}-290^{\circ} \\ & =70^{\circ} \\ & =70 \times \frac{3.142}{180} \\ & =1.222 \text { radians } \end{aligned} $$
(b)
$$ \begin{aligned} 16 & =r \times 1.222 \\ r & =\frac{16}{1.222} \\ & =13.09 \mathrm{~cm} \end{aligned} $$
Question 10 (SPM 2006):
Diagram 7 shows sector OAB with centre O and sector AXY with centre A.
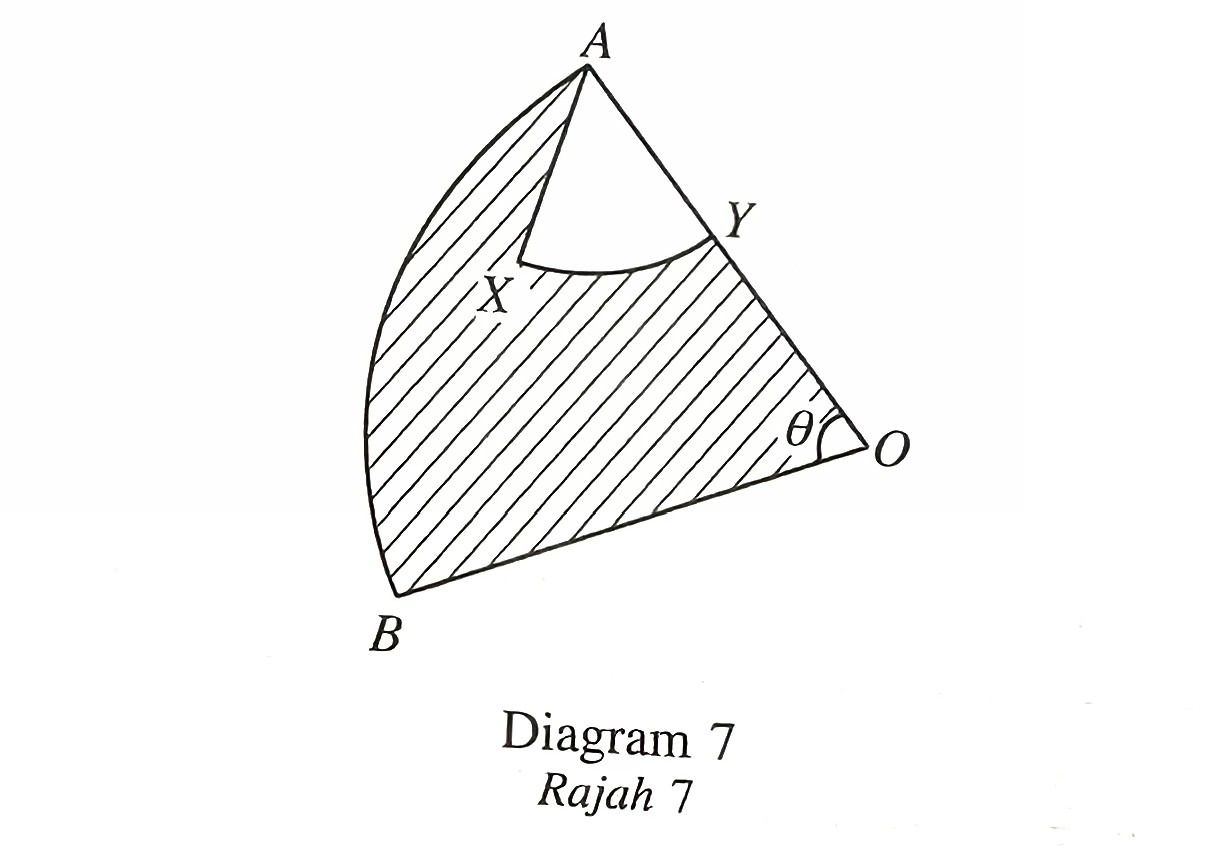 Given OB = 10 cm, AY = 4 cm, ∠XAY = 1.1 radians and the length of AB = 7 cm.
Given OB = 10 cm, AY = 4 cm, ∠XAY = 1.1 radians and the length of AB = 7 cm.
Calculate
(a) the value of θ, in radian.
(b) the area, in cm2, of the shaded region.
[4 marks]
Answer:
(a)
$$ \begin{aligned} 10 \theta & =7 \\ \theta & =0.7 \mathrm{rad} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Area of the shaded region } \\ & =\text { Area of sector } O A B \text { – Area of sector } A X Y \\ & =\frac{1}{2}\left(10^2\right)(0.7)-\frac{1}{2}\left(4^2\right)(1.1) \\ & =35-8.8 \\ & =26.2 \mathrm{~cm}^2 \end{aligned} $$
Diagram 7 shows sector OAB with centre O and sector AXY with centre A.
 Given OB = 10 cm, AY = 4 cm, ∠XAY = 1.1 radians and the length of AB = 7 cm.
Given OB = 10 cm, AY = 4 cm, ∠XAY = 1.1 radians and the length of AB = 7 cm.Calculate
(a) the value of θ, in radian.
(b) the area, in cm2, of the shaded region.
[4 marks]
Answer:
(a)
$$ \begin{aligned} 10 \theta & =7 \\ \theta & =0.7 \mathrm{rad} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Area of the shaded region } \\ & =\text { Area of sector } O A B \text { – Area of sector } A X Y \\ & =\frac{1}{2}\left(10^2\right)(0.7)-\frac{1}{2}\left(4^2\right)(1.1) \\ & =35-8.8 \\ & =26.2 \mathrm{~cm}^2 \end{aligned} $$
Nice questions. Good revision.