SPM Additional Mathematics 2019, Paper 2 (Question 9)

Question 9:
Solution by scale drawing is not accepted.
Diagram 5 shows the path of a moving point P(x, y). P always moves at a constant distance from point A.

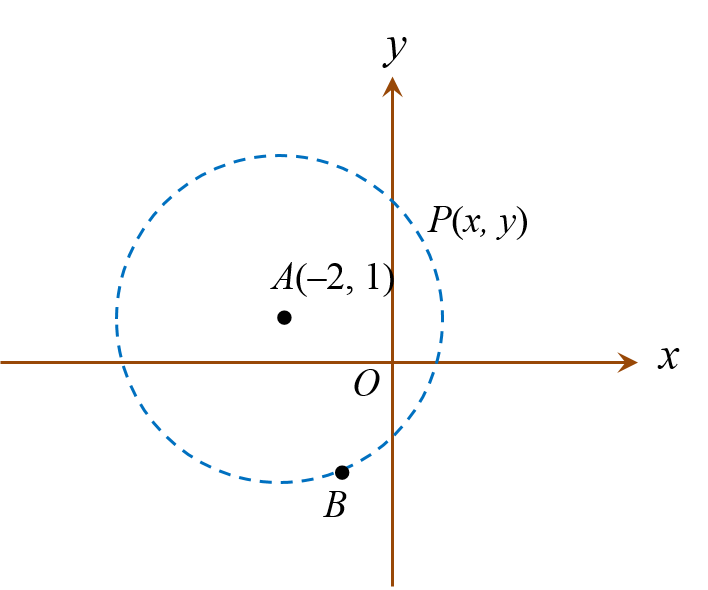Diagram 5

B(–1, –2) and R(–5, q) lie on path of point P. The straight line BC is a tangent to the path and
intersects the x-axis at point C.
Find
(a) the equation of the path of point P, [3 marks]
(b) the possible values of q, [2 marks]
(c) the area of ∆ ABC. [5 marks]

Solution:
(a)

\begin{matrix} Radius A B = \sqrt{{(- 2 + 1)}^{2} + {(1 + 2)}^{2}} = \sqrt{1 + 9} = \sqrt{10} P A = \sqrt{10} \sqrt{{(x + 2)}^{2} + {(y - 1)}^{2}} = \sqrt{10} {(x + 2)}^{2} + {(y - 1)}^{2} = 10 x^{2} + 4 x + 4 + y^{2} - 2 y + 1 - 10 = 0 x^{2} + y^{2} + 4 x - 2 y - 5 = 0 \end{matrix}

$\begin{array}{l} Radius A B = \sqrt{{(- 2 + 1)}^{2} + {(1 + 2)}^{2}} \\ = \sqrt{1 + 9} \\ = \sqrt{10} \\ P A = \sqrt{10} \\ \sqrt{{(x + 2)}^{2} + {(y - 1)}^{2}} = \sqrt{10} \\ {(x + 2)}^{2} + {(y - 1)}^{2} = 10 \\ x^{2} + 4 x + 4 + y^{2} - 2 y + 1 - 10 = 0 \\ x^{2} + y^{2} + 4 x - 2 y - 5 = 0 \end{array}$

(b)
When x = –5, y = q,
(–5)² + q² + 4(–5) – 2q – 5 = 0
25 + q² – 20 – 2q – 5 = 0
q² – 2q = 0
q(q – 2) = 0
q = 0, q = 2

(c)

\begin{matrix} m_{A B} \times m_{B C} = - 1 (\frac{1 + 2}{- 2 + 1}) \times m_{B C} = - 1 (\frac{3}{- 1}) \times m_{B C} = - 1 m_{B C} = \frac{1}{3} Equation of B C : y - (- 2) = \frac{1}{3} (x + 1) 3 (y + 2) = x + 1 3 y + 6 = x + 1 3 y = x - 5 At point C, y = 0 x - 5 = 0 x = 5 C = (5, 0) \end{matrix}

$\begin{array}{l} m_{A B} \times m_{B C} = - 1 \\ (\frac{1 + 2}{- 2 + 1}) \times m_{B C} = - 1 \\ (\frac{3}{- 1}) \times m_{B C} = - 1 \\ m_{B C} = \frac{1}{3} \\ Equation of B C : \\ y - (- 2) = \frac{1}{3} (x + 1) \\ 3 (y + 2) = x + 1 \\ 3 y + 6 = x + 1 \\ 3 y = x - 5 \\ At point C, y = 0 \\ x - 5 = 0 \\ x = 5 \\ C = (5, 0) \end{array}$

\begin{matrix} Area of Δ A B C = \frac{1}{2} ∣ ∣ ∣ \begin{matrix} 5 - 2 - 15 01 - 20 \end{matrix} ∣ ∣ ∣ = \frac{1}{2} | 5 + 4 + 0 - 0 - (- 1) - (- 10) | = \frac{1}{2} | 20 | = 10 {unit}^{2} \end{matrix}

$\begin{array}{l} Area of Δ A B C \\ = \frac{1}{2} | \begin{array}{l} 5 - 2 - 1 5 \\ 0 1 - 2 0 \end{array} | \\ = \frac{1}{2} | 5 + 4 + 0 - 0 - (- 1) - (- 10) | \\ = \frac{1}{2} | 20 | \\ = 10 {unit}^{2} \end{array}$

Leave a Comment Cancel reply