SPM Additional Mathematics 2019, Paper 2 (Question 13)

Question 13:
Solution by scale drawing is not accepted.
Diagram 6 shows a quadrilateral ABCD such that AC and BD are straight lines.

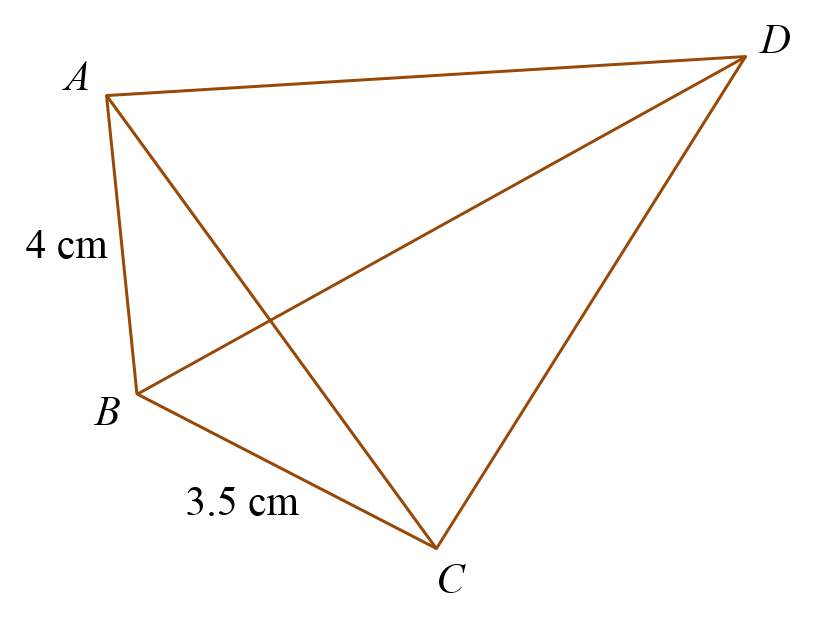Diagram 6

It is given that the area of ∆ABC = 6 cm² and ∠ABC is obtuse.
(a) Find
(i) ∠ABC,
(ii) the length, in cm, of AC,
(iii) ∠BAC [7 marks]
(b) Given BD = 7.3 cm and ∠BCD = 90°, calculate the area in cm², of ∆ACD. [3 marks]

Solution:
(a)(i)

\begin{array}{l} Area of Δ A B C = 6 {cm}^{2} \\ \frac{1}{2} \times 4 \times 3.5 \times \sin ∠ A B C = 6 \\ ∠ A B C = 121^{o} \end{array}

(a)(ii)

\begin{array}{l} A C^{2} = 4^{2} + {3.5}^{2} - 2 (4) (3.5) \cos 121^{o} \\ A C = 6.532 cm \end{array}

(a)(iii)

\begin{array}{l} \frac{\sin ∠ B A C}{3.5} = \frac{\sin 121}{6.532} \\ \sin ∠ B A C = \frac{3.5 \times \sin 121}{6.532} \\ ∠ B A C = 27^{o} 20 ‘ \end{array}

(b)

\begin{array}{l} \cos ∠ C B D = \frac{3.5}{7.3} \\ ∠ C B D = 61^{o} 21 ‘ \\ ∠ A B D = 121^{o} - 61^{o} 21 ‘ \\ = 59^{o} 39 ‘ \\ Area of Δ A C D \\ = Area of Δ C B D + Area of Δ A B D - 6 \\ = (\frac{1}{2} \times 3.5 \times 7.3 \times \sin 61^{o} 21 ‘) + (\frac{1}{2} \times 4 \times 7.3 \times \sin 59^{o} 39 ‘) - 6 \\ = 18.434 {cm}^{2} - 6 \\ = 12.434 {cm}^{2} \end{array}

Leave a Comment Cancel reply