Question 9:
Diagram 4 shows a circle ADBC, with centre O and diameter 12 cm while sector ADC with the centre A and radius AD = 10 cm.
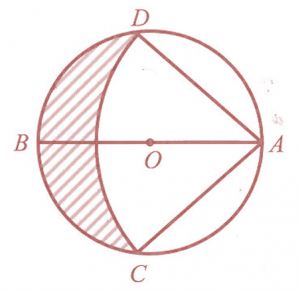 Diagram 4
Diagram 4
By using π = 3.142,
find
(a) ∠BAC in radians, (2 marks)
(b) area, in cm2, of the shaded region. (3 marks)
Solution:
(a)
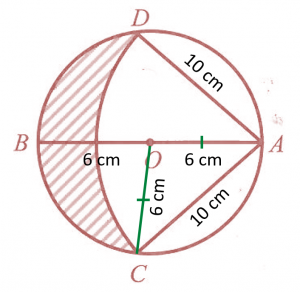
(b)
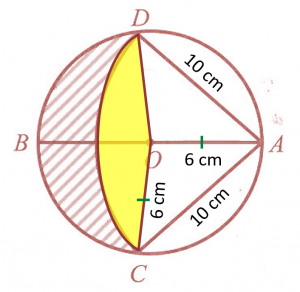
Diagram 4 shows a circle ADBC, with centre O and diameter 12 cm while sector ADC with the centre A and radius AD = 10 cm.
 Diagram 4
Diagram 4By using π = 3.142,
find
(a) ∠BAC in radians, (2 marks)
(b) area, in cm2, of the shaded region. (3 marks)
Solution:
(a)

(b)
