6.1 Positive and Negative Angles
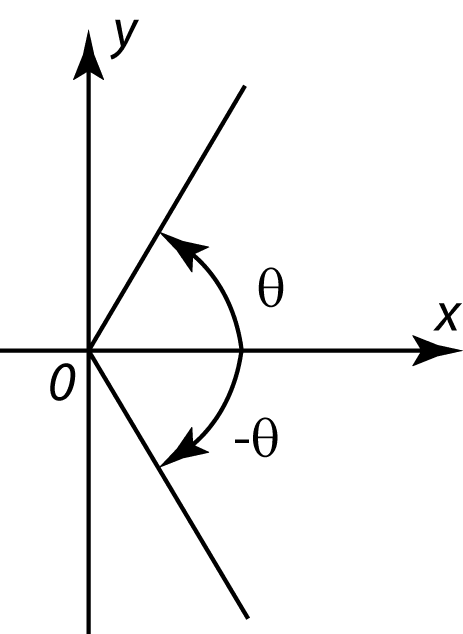
1. Positive angles are angles measure in an anticlockwise rotate from the positive x-axis about the origin, O.
2. Negative angles are angles measured in a clockwise rotation from the positive x-axis about the origin O.
3. One complete revolution is 360° or 2π radians.
Example:
Show each of the following angles on a separate diagram and state the quadrant in which the angle is situated.
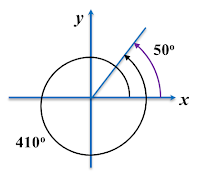
(a) 410°
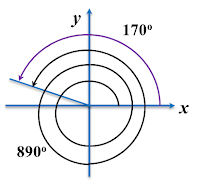
(b) 890°
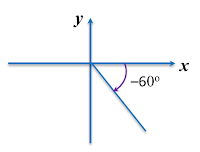
(e) –60o
(f) –500°
Solution:
(a)
Based on the above circular diagram, the positive angle of 410° is in the first quadrant.
(b)
Based on the above circular diagram, the positive angle of 890° is in the second quadrant.
(c)
Based on the above circular diagram, the positive angle of
is in the first quadrant.
(d)
Based on the above circular diagram, the positive angle of
is in the third quadrant.
(e)
Based on the above circular diagram, the negative angle of –60° is in the fourth quadrant.
(f)
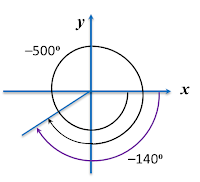
–500° = –360° – 140°
Based on the above circular diagram, the negative angle of –500° is in the third quadrant.
(g)
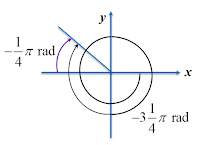
Based on the above circular diagram, the negative angle of
is in the second quadrant.