Question 10:
(a) It is found that 60% of the students from a certain class obtained grade A in English in O level trial examination.
If 10 students from the class are selected at random, find the probability that
(i) exactly 7 students obtained grade A.
(ii) not more than 7 students obtained grade A.
(b) Diagram below shows a standard normal distribution graph representing the volume of soy sauce in bottles produced by a factory.
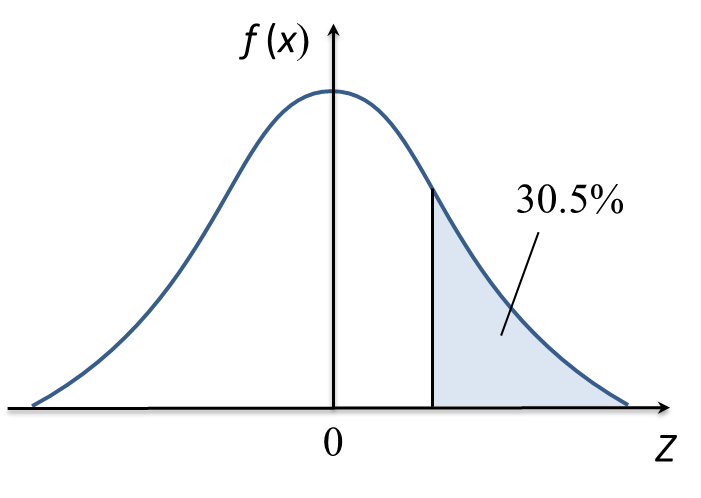It is given the mean is 950 cm3 and the variance is 256 cm6. If the percentage of the volume more than V is 30.5%, find
(i) the value of V,
(ii) the probability that the volume between 930 cm3 and 960 cm3.
Solution:
(a)(i)P(X=r)=cnr.pr.qn−rP(X=7)=C107(0.6)7(0.4)3 =0.0860(ii)P(X≤7)=1−P(X>7)=1−P(X=8)−P(X=9)−P(X=10)=1−C108(0.6)8(0.4)2−C109(0.6)9(0.4)1−C1010(0.6)10(0.4)0=1−0.1209−0.0403−0.0060=0.8328
(b)(i)P(X>V)=30.5%P(Z>V−95016)=0.305P(Z>0.51)=0.305 V−95016=0.51V=0.51(16)+950 =958.16 cm3
(ii)Probability=P(930<X<960)=P(930−95016<Z<960−95016)=P(−1.25<Z<0.625)=1−P(Z>1.25)−P(Z>0.625)=1−0.1056−0.2660=0.6284
(a) It is found that 60% of the students from a certain class obtained grade A in English in O level trial examination.
If 10 students from the class are selected at random, find the probability that
(i) exactly 7 students obtained grade A.
(ii) not more than 7 students obtained grade A.
(b) Diagram below shows a standard normal distribution graph representing the volume of soy sauce in bottles produced by a factory.
It is given the mean is 950 cm3 and the variance is 256 cm6. If the percentage of the volume more than V is 30.5%, find(i) the value of V,
(ii) the probability that the volume between 930 cm3 and 960 cm3.
Solution:
(a)(i)P(X=r)=cnr.pr.qn−rP(X=7)=C107(0.6)7(0.4)3 =0.0860(ii)P(X≤7)=1−P(X>7)=1−P(X=8)−P(X=9)−P(X=10)=1−C108(0.6)8(0.4)2−C109(0.6)9(0.4)1−C1010(0.6)10(0.4)0=1−0.1209−0.0403−0.0060=0.8328
(b)(i)P(X>V)=30.5%P(Z>V−95016)=0.305P(Z>0.51)=0.305 V−95016=0.51V=0.51(16)+950 =958.16 cm3
(ii)Probability=P(930<X<960)=P(930−95016<Z<960−95016)=P(−1.25<Z<0.625)=1−P(Z>1.25)−P(Z>0.625)=1−0.1056−0.2660=0.6284
Question 11:
(a) 20% of the students in SMK Bukit Bintang are cycling to school. If 9 pupils from the school are chosen at random, calculate the probability that
(i) exactly 3 of them are cycling to school,
(ii) at least a student is cycling to school. [4 marks]
(i) exactly 3 of them are cycling to school,
(ii) at least a student is cycling to school. [4 marks]
(b) The volume of 800 bottles of fresh milk produced by a factory follows a normal distribution with a mean of 520 ml per bottle and variance of 1600 ml2.
(i) Find the probability that a bottle of fresh milk chosen in random has a volume of less than 515 ml.
(ii) If 480 bottles out of 800 bottles of the fresh milk have volume greater that k ml, find the value of k. [6 marks]
(i) Find the probability that a bottle of fresh milk chosen in random has a volume of less than 515 ml.
(ii) If 480 bottles out of 800 bottles of the fresh milk have volume greater that k ml, find the value of k. [6 marks]
Solution:
(a)(i)
X~ Students in SMK Bukit Bintang who are cycling to school
X~ B (n, p)
X~ B (9, 0.2)
P (X = r) = nCr. pr. qn-r
Probability, exactly 3 students are cycling to school
P (X = 3) = 9C3(0.2)3 (0.8)6
= 0.1761
(a)(ii)
At least a student is cycling to school
= 1 – P (X = 0)
= 1 – 9C0 (0.2)0(0.8)9
= 0.8658
(b)(i)
m = 520 ml
σ2 = 1600 ml2
σ = 40
Let X represents volume of a bottle of fresh milk.
X ~ N (520, 1600)
P (X < 515)
=P(Z<515−52040)
= P (Z< – 0.125)
= P (Z> 0.125)
= 0.4502
(b)(ii)
P(X>k)=480800P(Z>k−52040)=0.6k−52040=−0.253k−520=−10.12k=509.88