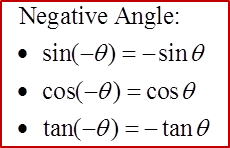6.2a Six Trigonometric Functions of Any Angle
(A) The definition of sin, cos, tan, cosec, sec and cot
(A) The definition of sin, cos, tan, cosec, sec and cot
1. Let P (x, y) be any point on the circumference of the circle with centre O and of radius r. Based on ∆ OPQ in the above diagram,
2. The definitions of tangent, cotangent, secant and cosecant of any angle are:
3. The relations of the trigonometric ratio of an angle θ with its complementary angle (90o – θ) are:
For examples:
(a) sin 75o = cos (90o – 75o) = cos 15o
(b) tan 50o = cot (90o – 50o) = cot 40o
(c) sec 25o= cosec (90o – 25o) = cosec 65o
4. The trigonometric ratios of any negative angle (–θ) are:
- A negative angle is an angle measured in a clockwise direction from the positive x-axis.
- For example, – 60ois equivalent to 300o (360o – 60o).
Example:
Express each of the following trigonometric functions in terms of the trigonometric ratios of acute angles. Hence, find each value using a calculator.
(a) cos (– 325o)
(b) tan (– 124o)
(c) sin (– 115o)
Solution:
(a)
cos (– 325o)
= cos 325o ← {The formula cos (–θ) = cos θ is used}
= cos (360o– 325o) ← {At fourth quadrant, cos is positive}
= cos 35o
= 0.8192
(b)
tan (– 124o)
= – tan 124o ← {The formula tan (–θ) = – tan θ is used}
= – [– tan (180o– 124o)] ← {At second quadrant, tan is negative}
= tan 56o
= 1.483
(c)
sin (– 115o)
= – sin 115o ← {The formula sin (–θ) = – sin θ is used}
= – sin (180o– 115o) ← {At second quadrant, sin is positive}
= – sin 65o
= – 0.9063