Question 7:
Diagram below shows a quadrilateral ABCD where the sides AB and CD are parallel. ∠BAC is an obtuse angle.
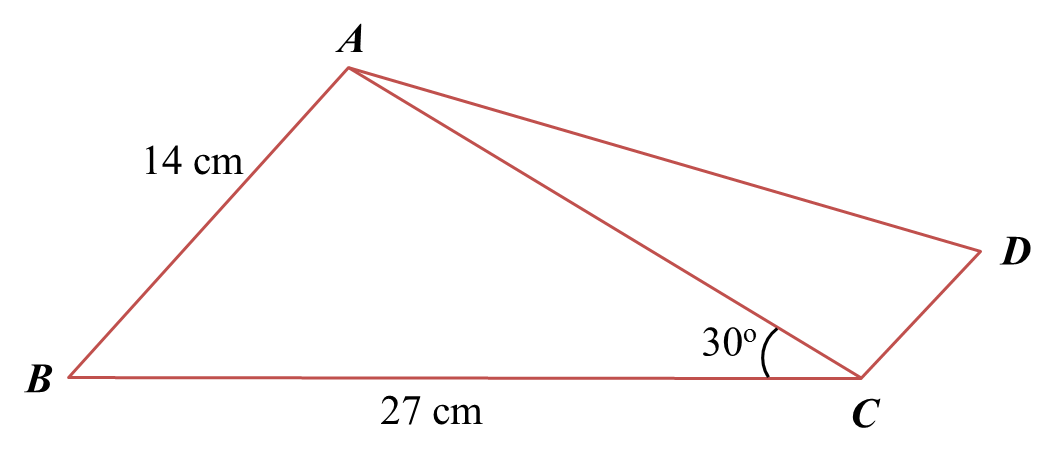
Given that AB = 14 cm, BC = 27 cm, ∠ACB = 30o and AB : DC = 7 : 3.
Calculate
(a) ∠BAC.
(b) the length, in cm, of diagonal BD.
(c) the area, in cm2, of quadrilateral ABCD.
Solution:
(a)
(b)
(c)
Diagram below shows a quadrilateral ABCD where the sides AB and CD are parallel. ∠BAC is an obtuse angle.

Given that AB = 14 cm, BC = 27 cm, ∠ACB = 30o and AB : DC = 7 : 3.
Calculate
(a) ∠BAC.
(b) the length, in cm, of diagonal BD.
(c) the area, in cm2, of quadrilateral ABCD.
Solution:
(a)
(b)
(c)
Question 8:
Diagram below shows a cyclic quadrilateral PQRS.
 (a) Calculate
(a) Calculate
(i) the length, in cm, of PR,
(ii) ∠PRQ.
(b) Find
(i) the area, in cm2, of ∆ PRS,
(ii) the short distance, in cm, from point S to PR.
Solution:
(a)(i)
(a)(ii)
(b)(i)
(b)(ii)
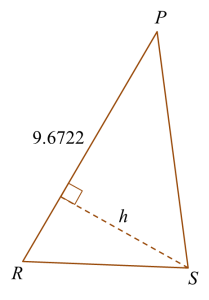
Diagram below shows a cyclic quadrilateral PQRS.
 (a) Calculate
(a) Calculate(i) the length, in cm, of PR,
(ii) ∠PRQ.
(b) Find
(i) the area, in cm2, of ∆ PRS,
(ii) the short distance, in cm, from point S to PR.
Solution:
(a)(i)
(a)(ii)
(b)(i)
(b)(ii)
