Question 9
Diagram 6 shows a quadrilateral KLMN.
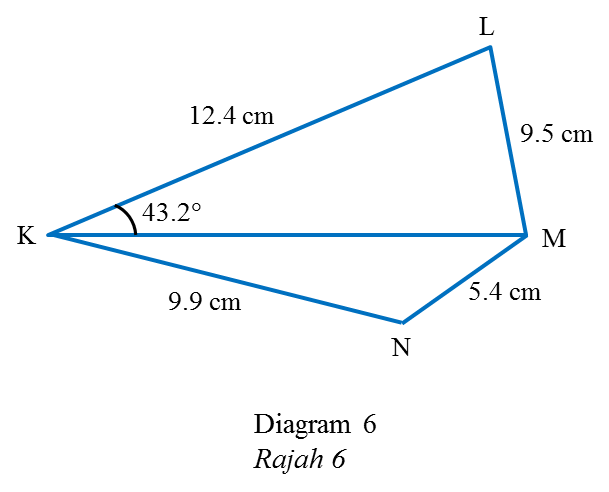

Calculate
(a) ∠KML, [2 marks]
(b) the length, in cm, of KM, [3 marks]
(c) area, in cm2, of triangle KMN, [3 marks]
(d) a triangle K’L’M’ has the same measurements as those given for triangle KLM, that is K’L’= 12.4 cm, L’M’= 9.5 cm and ∠L’K’M’= 43.2o, which is different in shape to triangle KLM.
(i) Sketch the triangle K’L’M’,
(ii) State the size of ∠K’M’L’. [2 marks]
(d) a triangle K’L’M’ has the same measurements as those given for triangle KLM, that is K’L’= 12.4 cm, L’M’= 9.5 cm and ∠L’K’M’= 43.2o, which is different in shape to triangle KLM.
(i) Sketch the triangle K’L’M’,
(ii) State the size of ∠K’M’L’. [2 marks]
Solution:
(a)
(b)
∠KLM = 180o – 43.2o – 63.32o = 73.48o
KM2 = 9.52 + 12.42 – 2(9.5)(12.4) cos 73.48o
KM2 = 244.01 – 66.99
KM2 = 177.02
KM = 13.30 cm
(c)
KM2 = MN2+ KN2– 2(MN)(KN) cos ∠KNM
13.302 = 5.42 + 9.92– 2(5.4)(9.9) cos ∠KNM
176.89 = 127.17 – 106.92 cos ∠KNM
Area of triangle KMN
(d)(i)
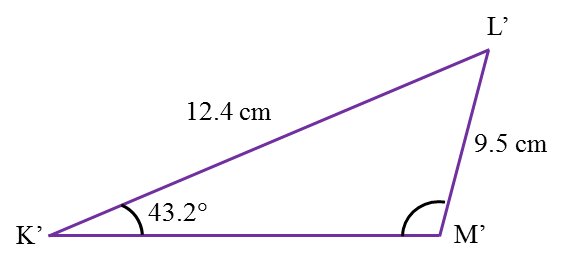

(d)(ii)
∠K’M’L’ = 180o – 63.32o = 116.68o