Question 3:
Solution:
(a)
(b)
∠RQS = 180o – 85o – 28o
(c)
(d)
Area of triangle QRS

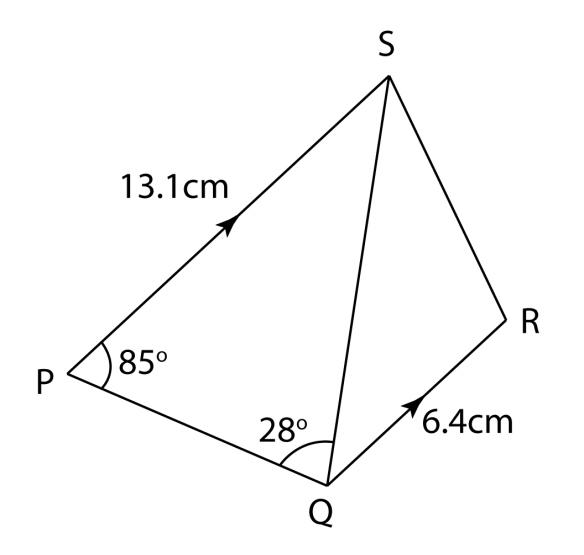
The diagram shows a trapezium PQRS. PS is parallel to QR and QRS is obtuse. Find
(a) the length, in cm, of QS,
(b) the length, in cm, of RS,
(c) ∠QRS,
(d) the area, in cm2, of triangle QRS.
(a)
(b)
∠RQS = 180o – 85o – 28o
∠RQS = 67o
Using cosine rule,
RS2 = QR2 + QS2 – 2 (QR)(QS) ∠RQS
RS2 = 6.42 + 27.82 – 2 (6.4)(27.8) cos 67o
RS2 = 813.8 – 139.04
RS2 = 674.76
RS = 25.98 cm
(c)
(d)
Area of triangle QRS
= ½ (QR)(RS) sin R
= ½ (6.4) (25.98) sin 99.86o
= 81.91 cm2
Question 4:
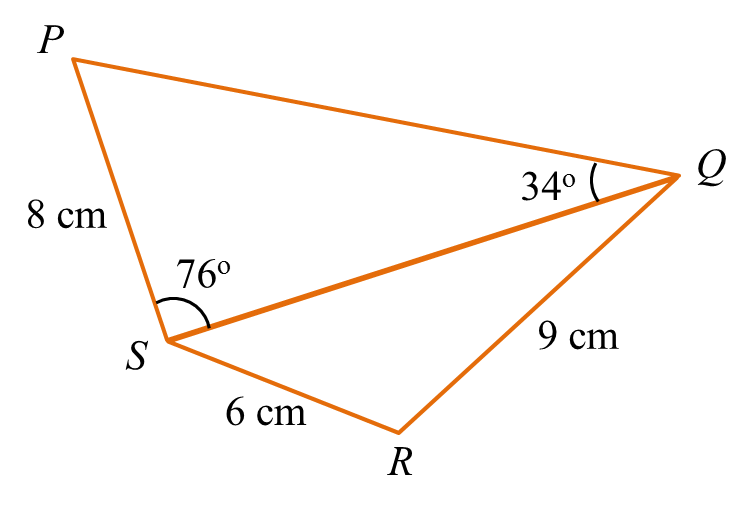
Diagram below shows a quadrilateral PQRS.
(a) Find
(i) the length, in cm, of QS.
(ii) ∠QRS.
(iii) the area, in cm2, of the quadrilateral PQRS.
(b)(i) Sketch a triangle S’Q’R’ which has a different shape from triangle SQR such that S’R’ = SR, S’Q’ = SQ and ∠S’Q’R’ = ∠SQR.
(ii) Hence, state ∠S’R’Q’.
Solution:
(a)(i)
(a)(ii)
(a)(iii)
(b)(i)
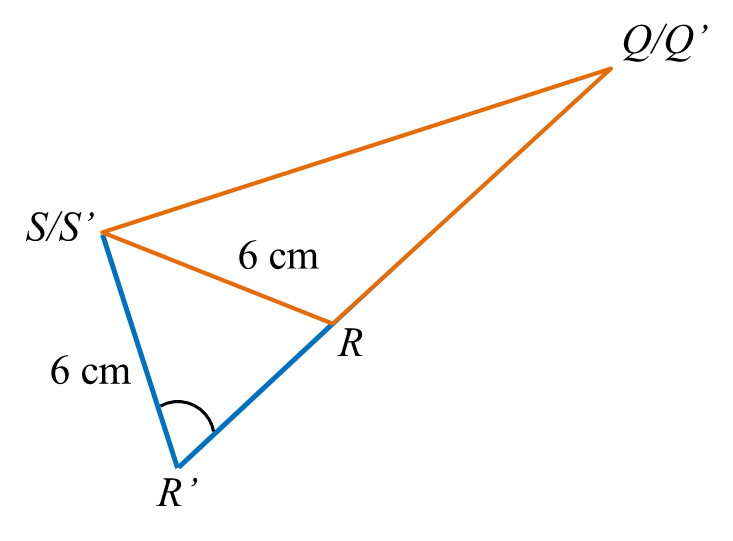
(b)(ii)
Diagram below shows a quadrilateral PQRS.

(a) Find
(i) the length, in cm, of QS.
(ii) ∠QRS.
(iii) the area, in cm2, of the quadrilateral PQRS.
(b)(i) Sketch a triangle S’Q’R’ which has a different shape from triangle SQR such that S’R’ = SR, S’Q’ = SQ and ∠S’Q’R’ = ∠SQR.
(ii) Hence, state ∠S’R’Q’.
Solution:
(a)(i)
(a)(ii)
(a)(iii)
(b)(i)

(b)(ii)