9.4.1 Solution of Triangles Long Questions (Question 1 & 2)

Question 1:

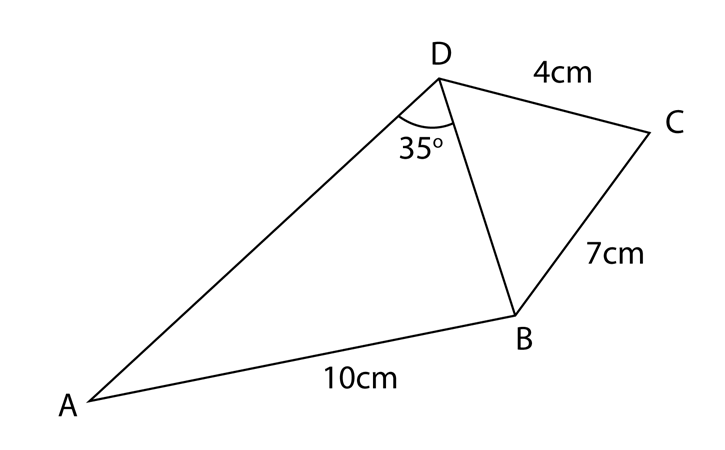
The diagram shows a quadrilateral ABCD. The area of triangle BCD is 12 cm² and ∠BCD is acute. Calculate

(a) ∠BCD,

(b) the length, in cm, of BD,

(c) ∠ABD,

(d) the area, in cm², quadrilateral ABCD.

Solution:

(a) Given area of triangle BCD = 12 cm²

½ (BC)(CD) sin C = 12

½ (7) (4) sin C = 12

14 sin C = 12

sin C = 12/14 = 0.8571

C = 59^o

∠BCD = 59^o

(b)
Using cosine rule,

BD² = BC² + CD² – 2 (7)(4) cos 59^o

BD² = 7²+ 4² – 2 (7)(4) cos 59^o

BD² = 65 – 28.84

BD² = 36.16

BD = 36.16
BD = 6.013 cm

(c)
Using sine rule,

\begin{array}{l} \frac{A B}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \frac{10}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \sin A = \frac{6.013 \times \sin 35^{\circ}}{10} \\ \sin A = 0.3449 \\ A = {20.18}^{\circ} \\ ∠ A B D = 180^{\circ} - 35^{\circ} - {20.18}^{\circ} \\ ∠ A B D = {124.82}^{\circ} \end{array}

(d)
Area of quadrilateral ABCD

= Area of triangle ABD + Area of triangle BCD

= ½ (AB)(BD) sin B + 12 cm

= ½ (10) (6.013) sin 124.82 + 12

= 24.68 + 12

= 36.68 cm²

Question 2:

In the diagram below, ABC is a triangle. AGJB, AHC and BKC are straight lines. The straight line JK is perpendicular to BC.

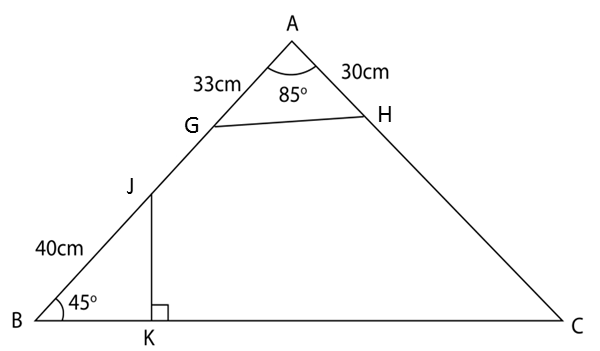
It is given that BG= 40cm, GA = 33 cm, AH = 30 cm, GAH = 85^o and JBK= 45^o.

(a) Calculate the length, in cm of

i. GH

ii. HC

(b) The area of triangle GAH is twice the area of triangle JBK. Calculate the length, in cm,

of BK.

(c) Sketch triangle which has a different shape from triangle ABC such that, A’B’ = AB,

A’C’ = AC and ∠A’B’C’ = ∠ABC.

Solution:
(a)(i)

Using cosine rule,

GH² = AG² + AH² – 2 (AG)(AH) ∠GAH

GH²= 33²+ 30² – 2 (33)(30) cos 85^o

GH² = 1089 + 900 – 172.57

GH² = 1816.43

GH = 42.62 cm

(a)(ii)

\begin{array}{l} ∠ A C D = 180^{\circ} - 45^{\circ} - 85^{\circ} = 50^{\circ} \\ Using sine rule, \\ \frac{A C}{\sin 45^{\circ}} = \frac{73}{\sin 50^{\circ}} \\ A C = \frac{73 \times \sin 45^{\circ}}{\sin 50^{\circ}} \\ A C = 67.38 cm \\ ∴ H C = 67.38 - 30 = 37.38 cm \end{array}

(b)

\begin{array}{l} Area of Δ G A H = \frac{1}{2} (33) (30) \sin 85^{\circ} = 493.12 {cm}^{2} \\ Let length of B K = J K = x \\ 2 \times Area of Δ J B K = Area of Δ G A H \\ 2 \times [\frac{1}{2} (x) (x)] = 493.12 \\ x^{2} = 493.12 \\ x = 22.21 cm \\ B K = 22.21 cm \end{array}

(c)