8.7.2 Vector, Long Questions (Question 3 & 4)

Question 3:

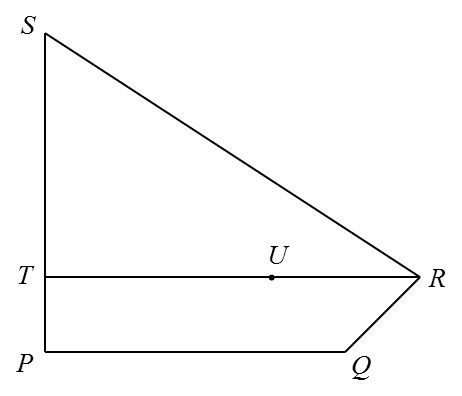
In diagram below, PQRS is a quadrilateral. PTS and TUR are straight lines.

It is given that

\vec{P Q} = 20 \underset{˜}{x}, \vec{P T} = 8 \underset{˜}{y}, \vec{S R} = 25 \underset{˜}{x} - 24 \underset{˜}{y}, \vec{P T} = \frac{1}{4} \vec{P S} and \vec{T U} = \frac{3}{5} \vec{T R}

(a) Express in terms of

\underset{˜}{x}

and/or

\underset{˜}{y}

(i) $\vec{Q S}$
(ii) $\vec{T R}$
(b) Show that the points Q, U and S are collinear.

(c) If

| \underset{˜}{x} |

= 2 and

| \underset{˜}{y} |

= 3, find

| \vec{Q S} |

Solution:
(a)(i)

\begin{array}{l} \vec{Q S} = \vec{Q P} + \vec{P S} \\ \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \leftarrow \begin{array}{l} Given \vec{P T} = \frac{1}{4} \vec{P S} \\ \vec{P S} = 4 \vec{P T} = 4 (8 \underset{˜}{y}) = 32 \underset{˜}{y} \end{array} \end{array}

(a)(ii)

\begin{array}{l} \vec{T R} = \vec{T S} + \vec{S R} \\ \vec{T R} = \frac{3}{4} \vec{P S} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = \frac{3}{4} (32 \underset{˜}{y}) + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 24 \underset{˜}{y} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 25 \underset{˜}{x} \end{array}

(b)

\begin{array}{l} \vec{Q U} = \vec{Q P} + \vec{P T} + \vec{T U} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + \frac{3}{5} (25 \underset{˜}{x}) \leftarrow \begin{array}{l} Given \\ \vec{T U} = \frac{3}{5} \vec{T R} \end{array} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + 15 \underset{˜}{x} \\ \vec{Q U} = - 5 \underset{˜}{x} + 8 \underset{˜}{y} \\ From (a)(i) \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{- 20 \underset{˜}{x} + 32 \underset{˜}{y}}{- 5 \underset{˜}{x} + 8 \underset{˜}{y}} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{4 (- 5 \underset{˜}{x} + 8 \underset{˜}{y})}{(- 5 \underset{˜}{x} + 8 \underset{˜}{y})} \\ \frac{\vec{Q S}}{\vec{Q U}} = 4 \\ \vec{Q S} = 4 \vec{Q U} \\ ∴ Q, U and S are collinear . \end{array}

(c)

\begin{array}{l} \vec{P S} = 32 \underset{˜}{y} \\ | \vec{P S} | = 32 | \underset{˜}{y} | \\ | \vec{P S} | = 32 \times 3 = 96 \\ \vec{P Q} = 20 \underset{˜}{x} \\ | \vec{P Q} | = 20 | \underset{˜}{x} | \\ | \vec{P Q} | = 20 \times 2 = 40 \\ ∴ | \vec{Q S} | = \sqrt{96^{2} + 40^{2}} \\ | \vec{Q S} | = 104 \end{array}

Question 4:
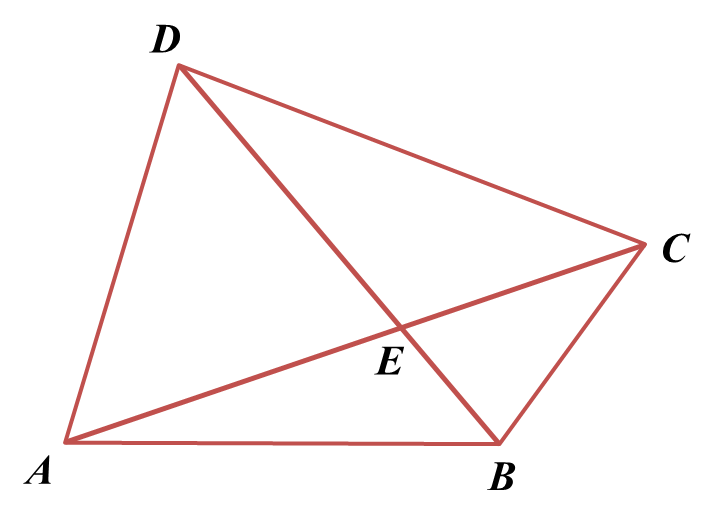
Diagram below shows quadrilateral ABCD. The straight line AC intersects the straight line BD at point E.

\begin{array}{l} It is given that B E : E D = 2 : 3, \vec{A B} = 10 \underset{˜}{x}, \vec{A D} = 25 \underset{˜}{y} and \vec{B C} = - \underset{˜}{x} + 15 \underset{˜}{y} . \\ (a) Express in terms of \underset{˜}{x} and \underset{˜}{y}, \\ (i) \vec{B D} \\ (ii) \vec{A E} \\ (b) Find the ratio A E : E C . \end{array}

Solution:
(a)(i)

\begin{array}{l} \vec{B D} = \vec{B A} + \vec{A D} \\ = \vec{A D} - \vec{A B} \\ = 25 \underset{˜}{y} - 10 \underset{˜}{x} \end{array}

(a)(ii)

\begin{array}{l} \vec{A E} = \vec{A B} + \vec{B E} \\ = \vec{A B} + \frac{2}{5} \vec{B D} \\ = 10 \underset{˜}{x} + \frac{2}{5} (25 \underset{˜}{y} - 10 \underset{˜}{x}) \\ = 10 \underset{˜}{x} + \frac{2}{5} (25 \underset{˜}{y} - 10 \underset{˜}{x}) \\ = 10 \underset{˜}{x} + 10 \underset{˜}{y} - 4 \underset{˜}{x} \\ = 6 \underset{˜}{x} + 10 \underset{˜}{y} \\ = 2 (3 \underset{˜}{x} + 5 \underset{˜}{y}) \end{array}

(b)

\begin{array}{l} \vec{E C} = \vec{E B} + \vec{B C} \\ = \vec{B C} - \vec{B E} \\ = \vec{B C} - \frac{2}{3} \vec{E D} \\ = \vec{B C} - \frac{2}{3} (\vec{E A} + \vec{A D}) \\ = - \underset{˜}{x} + 15 \underset{˜}{y} - \frac{2}{3} (- 6 \underset{˜}{x} - 10 \underset{˜}{y} + 25 \underset{˜}{y}) \\ = - \underset{˜}{x} + 15 \underset{˜}{y} - \frac{2}{3} (- 6 \underset{˜}{x} + 15 \underset{˜}{y}) \\ = - \underset{˜}{x} + 15 \underset{˜}{y} + 4 \underset{˜}{x} - 10 \underset{˜}{y} \\ = 3 \underset{˜}{x} + 5 \underset{˜}{y} \\ \frac{A E}{E C} = \frac{2 (3 \underset{˜}{x} + 5 \underset{˜}{y})}{1 (3 \underset{˜}{x} + 5 \underset{˜}{y})} \\ A E : E C = 2 : 1 \end{array}