\

7.8.2 Coordinate Geometry Long Questions (Question 3 & 4)


Question 3:
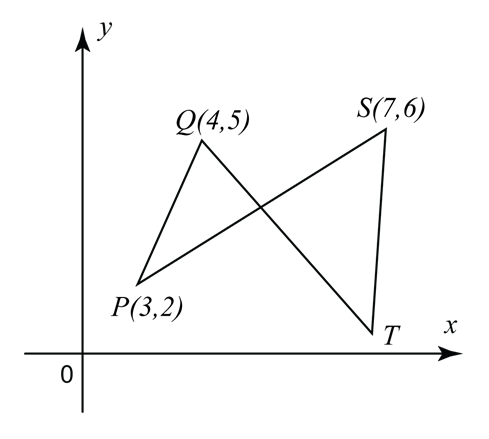In the diagram, PRS and QRT are straight lines. Given R is the midpoint of PS and
QR : RT = 1 : 3, Find
(a) the coordinates of R,
(b) the coordinates of T,
(c) the coordinates of the point of intersection between lines PQ and ST produced.

Solution:
(a)
Given R is the midpoint of PS.
R = ( 3 + 7 2 , 2 + 6 2 ) R = ( 5 ,   4 )

(b)
Q R : R T = 1 : 3 Lets coordinates of  T = ( x ,   y ) ( ( 1 ) ( x ) + ( 3 ) ( 4 ) 1 + 3 , ( 1 ) ( y ) + ( 3 ) ( 5 ) 1 + 3 ) = ( 5 ,  4 ) x + 12 4 = 5 x + 12 = 20 x = 8 y + 15 4 = 4 y + 15 = 16 y = 1 T = ( 8 ,   1 )


(c)
Gradient of  P Q = 5 − 2 4 − 3 = 3 Equation of  P Q , y − 2 = 3 ( x − 3 ) y − 2 = 3 x − 9 y = 3 x − 7 − − − − ( 1 ) Gradient of  S T = 6 − 1 7 − 8 = − 5 Equation of  S T , y − 1 = − 5 ( x − 8 ) y − 1 = − 5 x + 40 y = − 5 x + 41 − − − − ( 2 )
 
Substitute (1) into (2),
 3x – 7 = –5x + 41
 8x = 48
 x = 6

 From (1),
 y = 3(6) – 7 = 11 

The coordinates of the point of intersection between lines PQ and ST = (6, 11).



Question 4:

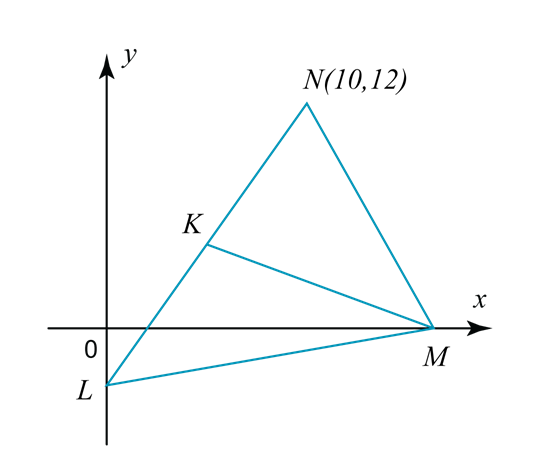
The diagram shows a triangle LMN where L is on the y-axis. The equation of the straight line LKN and MK are 2y – 3x + 6 = 0 and 3y + x– 13 = 0 respectively. Find
(a) the coordinates of K
(b) the ratio LK:KN



Solution:
(a)
2y – 3x + 6 = 0 —-(1)
3y + x – 13 = 0 —-(2)
x = 13 – 3y —-(3)

Substitute equation (3) into (1),
2y – 3 (13 – 3y) + 6 = 0
2y – 39 + 9y + 6 = 0
11y = 33
y = 3
Substitute y = 3 into equation (3),
x = 13 – 3 (3)
x = 4
Coordinates of K = (4, 3).


(b)
Given equation of LKN is 2y – 3x + 6 = 0
At y – axis, x = 0,
x coordinates of point L = 0.

Ratio  L K : K N Equating the  x  coordinates, L K ( 10 ) + K N ( 0 ) L K + K N = 4 10 L K = 4 L K + 4 K N 6 L K = 4 K N L K K N = 4 6 L K K N = 2 3 Ratio  L K : K N = 2 : 3

Leave a Comment