7.8.1 Coordinate Geometry Long Questions (Question 1 & 2)

Question 1:

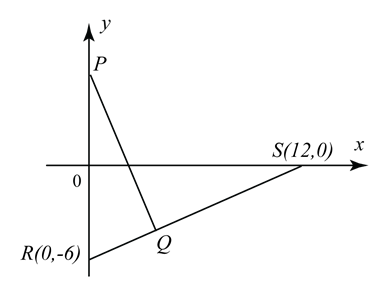
The diagram shows a straight line PQ which meets a straight line RS at the point Q. The point P lies on the y-axis.

(a) Write down the equation of RS in the intercept form.

(b) Given that 2RQ = QS, find the coordinates of Q.

(c) Given that PQ is perpendicular to RS, find the y-intercept of PQ.

Solution:

(a)

Equation of RS

\begin{array}{l} \frac{x}{12} + \frac{y}{- 6} = 1 \\ \frac{x}{12} - \frac{y}{6} = 1 \end{array}

(b)

\begin{array}{l} Given 2 R Q = Q S \\ \frac{R Q}{Q S} = \frac{1}{2} \\ Lets coordinates of Q = (x, y) \\ (\frac{(0) (2) + (12) (1)}{1 + 2}, \frac{(- 6) (2) + (0) (1)}{1 + 2}) = (x, y) \\ x = \frac{12}{3} = 4 \\ y = - \frac{12}{3} = - 4 \\ Q = (4, - 4) \end{array}

(c)

\begin{array}{l} Gradient of R S, m_{R S} \\ = - (\frac{- 6}{12}) = \frac{1}{2} \\ m_{P Q} = - \frac{1}{m_{R S}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Point Q = (4, –4), m = –2

Using y = mx+ c

–4 = –2 (4) + c

c = 4

y–intercept of PQ = 4

Question 2:

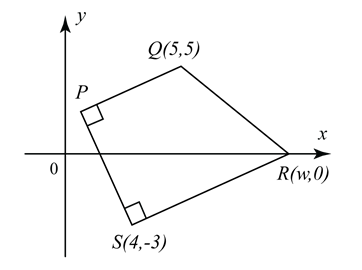
The diagram shows a trapezium PQRS. Given the equation of PQ is 2y – x – 5 = 0, find

(a) The value of w,

(b) the equation of PS and hence find the coordinates of P.

(c) The locus of M such that triangle QMS is always perpendicular at M.

Solution:
(a)

\begin{array}{l} Equation of P Q \\ 2 y - x - 5 = 0 \\ 2 y = x + 5 \\ y = \frac{1}{2} x + \frac{5}{2} \\ ∴ m_{P Q} = \frac{1}{2} \\ In a trapizium, m_{P Q} = m_{S R} \\ \frac{1}{2} = \frac{0 - (- 3)}{w - 4} \\ w - 4 = 6 \\ w = 10 \end{array}

(b)

\begin{array}{l} m_{P Q} = \frac{1}{2} \\ m_{P S} = - \frac{1}{m_{P Q}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Point S = (4, –3), m = –2

y – y₁ = m (x– x₁)

y – (–3) = –2 (x – 4)

y + 3 = –2x + 8

y = –2x + 5

Equation of PS is y = –2x + 5

PS is y = –2x + 5—–(1)

PQ is 2y = x + 5—–(2)

Substitute (1) into (2)

2 (–2x + 5) = x + 5

–4x + 10 = x + 5

–5x = –5

x = 1

From (1), y = –2(1) + 5

y = 3

Coordinates of point P = (1, 3).

(c)

\begin{array}{l} Let M = (x, y) \\ Given that △ Q M S is perpendicular at M \\ Thus △ Q M S = 90^{\circ} \\ (m_{Q M}) (m_{M S}) = - 1 \\ (\frac{y - 5}{x - 5}) (\frac{y - (- 3)}{x - 4}) = - 1 \\ (y - 5) (y + 3) = - 1 (x - 5) (x - 4) \\ y^{2} + 3 y - 5 y - 15 = - 1 (x^{2} - 4 x - 5 x + 20) \\ y^{2} - 2 y - 15 = - x^{2} + 9 x - 20 \\ x^{2} + y^{2} - 9 x - 2 y + 5 = 0 \end{array}

Hence, the equation of locus of the moving point M is

x² + y²– 9x – 2y + 5 = 0.