Question 31 (SPM 2019):
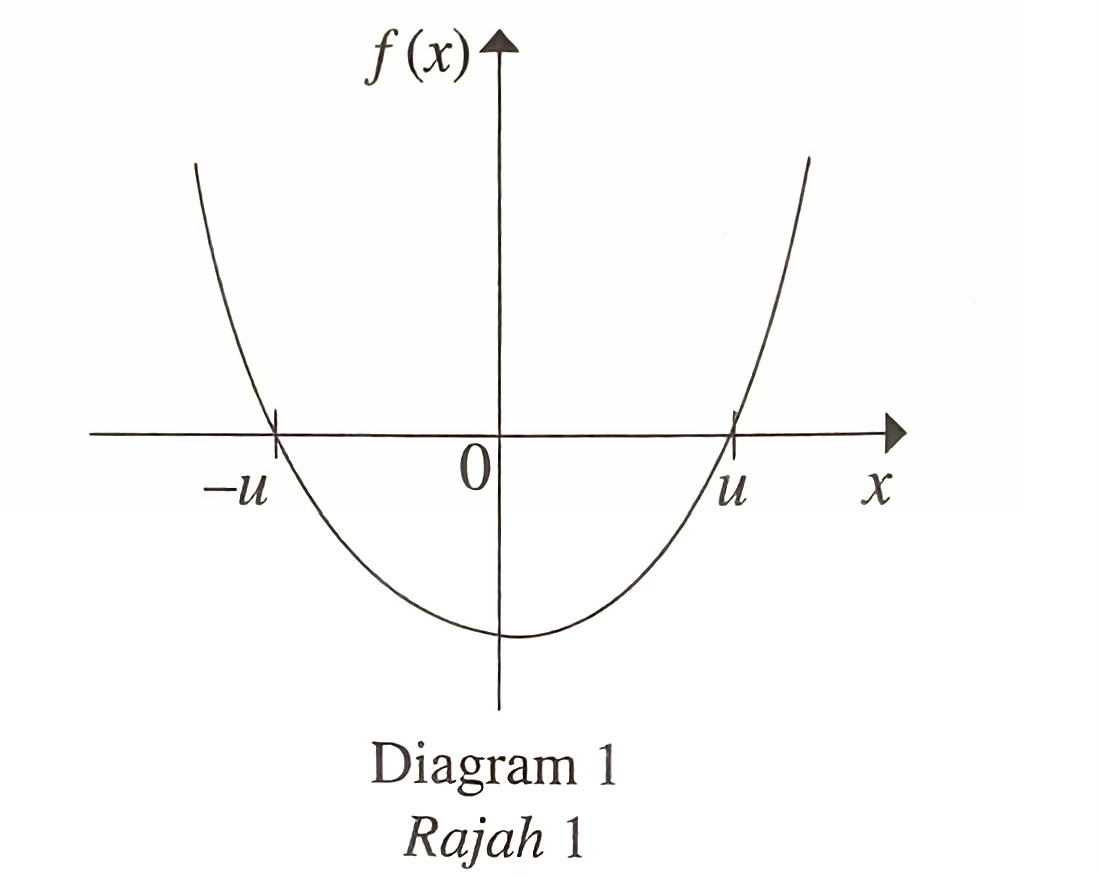
Diagram 1 shows the graph of a quadratic function
$$ f(x)=\frac{p}{x^n}+q x+r $$
such that p, q, r, n and u are constants.
 (a) State the value of n.
(a) State the value of n.
(b) If f(x) = 0 and the product of roots is r, state the value of
(i) q,
(ii) p.
[3 marks]
Answer:
(a)
$$ \begin{aligned} & x^{-n}=x^2 \\ & -n=2 \\ & n=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=p x^2+q x+r \\ & p x^2+q x+r=0 \\ & a=p, b=q, c=r \end{aligned} $$
$$ \begin{aligned} &\text { Product of Roots }=r\\ &\begin{aligned} & \frac{c}{a}=r \\ & \frac{r}{p}=r \\ & r=p r \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Sum of Roots }=-\frac{b}{a} \\ & u+(-u)=-\frac{q}{p} \\ & -\frac{q}{1}=0 \\ & q=0 \end{aligned} $$
$$ \begin{aligned} & r-p r=0 \\ & r(1-p)=0 \\ & r=0, p=1 \end{aligned} $$ (i) q = 0 (ii) p = 1
Diagram 1 shows the graph of a quadratic function
$$ f(x)=\frac{p}{x^n}+q x+r $$
such that p, q, r, n and u are constants.
 (a) State the value of n.
(a) State the value of n.(b) If f(x) = 0 and the product of roots is r, state the value of
(i) q,
(ii) p.
[3 marks]
Answer:
(a)
$$ \begin{aligned} & x^{-n}=x^2 \\ & -n=2 \\ & n=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=p x^2+q x+r \\ & p x^2+q x+r=0 \\ & a=p, b=q, c=r \end{aligned} $$
$$ \begin{aligned} &\text { Product of Roots }=r\\ &\begin{aligned} & \frac{c}{a}=r \\ & \frac{r}{p}=r \\ & r=p r \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Sum of Roots }=-\frac{b}{a} \\ & u+(-u)=-\frac{q}{p} \\ & -\frac{q}{1}=0 \\ & q=0 \end{aligned} $$
$$ \begin{aligned} & r-p r=0 \\ & r(1-p)=0 \\ & r=0, p=1 \end{aligned} $$ (i) q = 0 (ii) p = 1
Question 32 (SPM 2019):
The graph of a quadratic function f(x) = 3[2h – (x – 1)2], where h is a constant, has maximum point (1, h – 10).
(a) State the value of h.
(b) State the type of roots for f(x) = 0. Justify your answer.
[3 marks]
Answer:
(a)
$$ \begin{aligned} &f(x)=6 h-3(x-1)^2\\ &\text { Maximum value }=6 h \end{aligned} $$
$$ \begin{aligned} & h-10=6 h \\ & -10=5 h \\ & h=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=0 \\ & 6(-2)-3(x-1)^2=0 \\ & -12-3\left(x^2-2 x+1\right)=0 \\ & -12-3 x^2+6 x-3=0 \\ & 3 x^2-6 x+15=0 \\ & x^2-2 x+5=0 \\ & a=1, b=-2, c=5 \\ & \text { Value of } b^2-4 a c \\ & =(-2)^2-4(1)(5) \\ & =4-20 \\ & =-16 \\ & b^2-4 a c<0, \text { No roots } \end{aligned} $$
The graph of a quadratic function f(x) = 3[2h – (x – 1)2], where h is a constant, has maximum point (1, h – 10).
(a) State the value of h.
(b) State the type of roots for f(x) = 0. Justify your answer.
[3 marks]
Answer:
(a)
$$ \begin{aligned} &f(x)=6 h-3(x-1)^2\\ &\text { Maximum value }=6 h \end{aligned} $$
$$ \begin{aligned} & h-10=6 h \\ & -10=5 h \\ & h=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=0 \\ & 6(-2)-3(x-1)^2=0 \\ & -12-3\left(x^2-2 x+1\right)=0 \\ & -12-3 x^2+6 x-3=0 \\ & 3 x^2-6 x+15=0 \\ & x^2-2 x+5=0 \\ & a=1, b=-2, c=5 \\ & \text { Value of } b^2-4 a c \\ & =(-2)^2-4(1)(5) \\ & =4-20 \\ & =-16 \\ & b^2-4 a c<0, \text { No roots } \end{aligned} $$
Question 33 (SPM 2019):
It is given that the quadratic equation (px)2 + 5qx + 4 = 0 has two equal roots while the quadratic equation hx2 – x + p = 0 has no roots, where p, q and h are constants.
Express the range of q in terms of h.
[3 marks]
Answer:
$$ \begin{aligned} & (p x)^2+5 q x+4=0 \\ & p^2 x^2+5 q x+4=0 \\ & a=p^2, b=5 q, c=4 \\ & b^2-4 a c=0 \\ & (5 q)^2-4\left(p^2\right)(4)=0 \\ & 25 q^2-16 p^2=0 \end{aligned} $$
$$ \begin{aligned} & h x^2-x+p=0 \\ & a=h, b=-1, c=p \\ & b^2-4 a c<0 \\ & (-1)^2-4(h)(p)<0 \\ & 1-4 h p<0 \\ & 4 h p>1 \\ & p>\frac{1}{4 h} \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} & \text { From (1): } 16 p^2=25 q^2 \\ & p^2=\frac{25}{16} q^2 \\ & p= \pm \frac{5}{4} q \end{aligned}\\ &\text { Substitute (3) into (2) : } \end{aligned} $$
$$ \begin{aligned} & -\frac{5}{4} q>\frac{1}{4 h} \\ & q<-\frac{1}{5 h} \end{aligned} $$
OR $$ \begin{aligned} & \frac{5}{4} q>\frac{1}{4 h} \\ & q>\frac{1}{5 h} \end{aligned} $$
It is given that the quadratic equation (px)2 + 5qx + 4 = 0 has two equal roots while the quadratic equation hx2 – x + p = 0 has no roots, where p, q and h are constants.
Express the range of q in terms of h.
[3 marks]
Answer:
$$ \begin{aligned} & (p x)^2+5 q x+4=0 \\ & p^2 x^2+5 q x+4=0 \\ & a=p^2, b=5 q, c=4 \\ & b^2-4 a c=0 \\ & (5 q)^2-4\left(p^2\right)(4)=0 \\ & 25 q^2-16 p^2=0 \end{aligned} $$
$$ \begin{aligned} & h x^2-x+p=0 \\ & a=h, b=-1, c=p \\ & b^2-4 a c<0 \\ & (-1)^2-4(h)(p)<0 \\ & 1-4 h p<0 \\ & 4 h p>1 \\ & p>\frac{1}{4 h} \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} & \text { From (1): } 16 p^2=25 q^2 \\ & p^2=\frac{25}{16} q^2 \\ & p= \pm \frac{5}{4} q \end{aligned}\\ &\text { Substitute (3) into (2) : } \end{aligned} $$
$$ \begin{aligned} & -\frac{5}{4} q>\frac{1}{4 h} \\ & q<-\frac{1}{5 h} \end{aligned} $$
OR $$ \begin{aligned} & \frac{5}{4} q>\frac{1}{4 h} \\ & q>\frac{1}{5 h} \end{aligned} $$