Question 1:
It is given that four consecutive terms of a sequence are 50, 45, x and y. State the value of
(a) y – x if the sequence is an arithmetic progression,
(b) y/x if the sequence is a geometric progression.
[2 marks]
Solution:
(a)It is given that four consecutive terms of a sequence are 50, 45, x and y. State the value of
(a) y – x if the sequence is an arithmetic progression,
(b) y/x if the sequence is a geometric progression.
[2 marks]
Solution:
$$ \begin{aligned} & y-x=45-50 \\ & y-x=-5 \end{aligned} $$
(b)
$$ \begin{aligned} & \frac{y}{x}=\frac{45}{50} \\ & \frac{y}{x}=\frac{9}{10} \end{aligned} $$
Question 2:
Diagram 1 shows two straight lines.
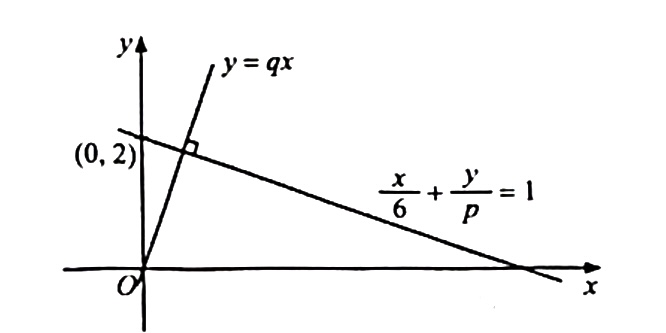
Find the value of q?
[3 marks]
Solution:
$$ \begin{aligned} &p \text { is the value of } y \text {-intercept. }\\ &\begin{aligned} & \therefore p=2 \\ & \frac{x}{6}+\frac{y}{2}=1 \\ & \frac{y}{2}=-\frac{x}{6}+1 \\ & y=-\frac{1}{3} x+2 \\ & \therefore m_1=-\frac{1}{3} \\ & y=q x \\ & \therefore m_2=q \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\frac{x}{6}+\frac{y}{2}=1 \text { is perpendicular to } y=q x\\ &\begin{aligned} m_1 m_2 & =-1 \\ \left(-\frac{1}{3}\right) \times(q) & =-1 \\ q & =3 \end{aligned} \end{aligned} $$
Diagram 1 shows two straight lines.

Find the value of q?
[3 marks]
Solution:
$$ \begin{aligned} &p \text { is the value of } y \text {-intercept. }\\ &\begin{aligned} & \therefore p=2 \\ & \frac{x}{6}+\frac{y}{2}=1 \\ & \frac{y}{2}=-\frac{x}{6}+1 \\ & y=-\frac{1}{3} x+2 \\ & \therefore m_1=-\frac{1}{3} \\ & y=q x \\ & \therefore m_2=q \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\frac{x}{6}+\frac{y}{2}=1 \text { is perpendicular to } y=q x\\ &\begin{aligned} m_1 m_2 & =-1 \\ \left(-\frac{1}{3}\right) \times(q) & =-1 \\ q & =3 \end{aligned} \end{aligned} $$
Question 3:
$$ \text { Diagram } 2 \text { shows two straight lines, } \mathrm{L}_1 \text { and } \mathrm{L}_2 \text {, drawn based on five plotted points on a plane } \frac{1}{y} \text { against } x^2 \text {. } $$
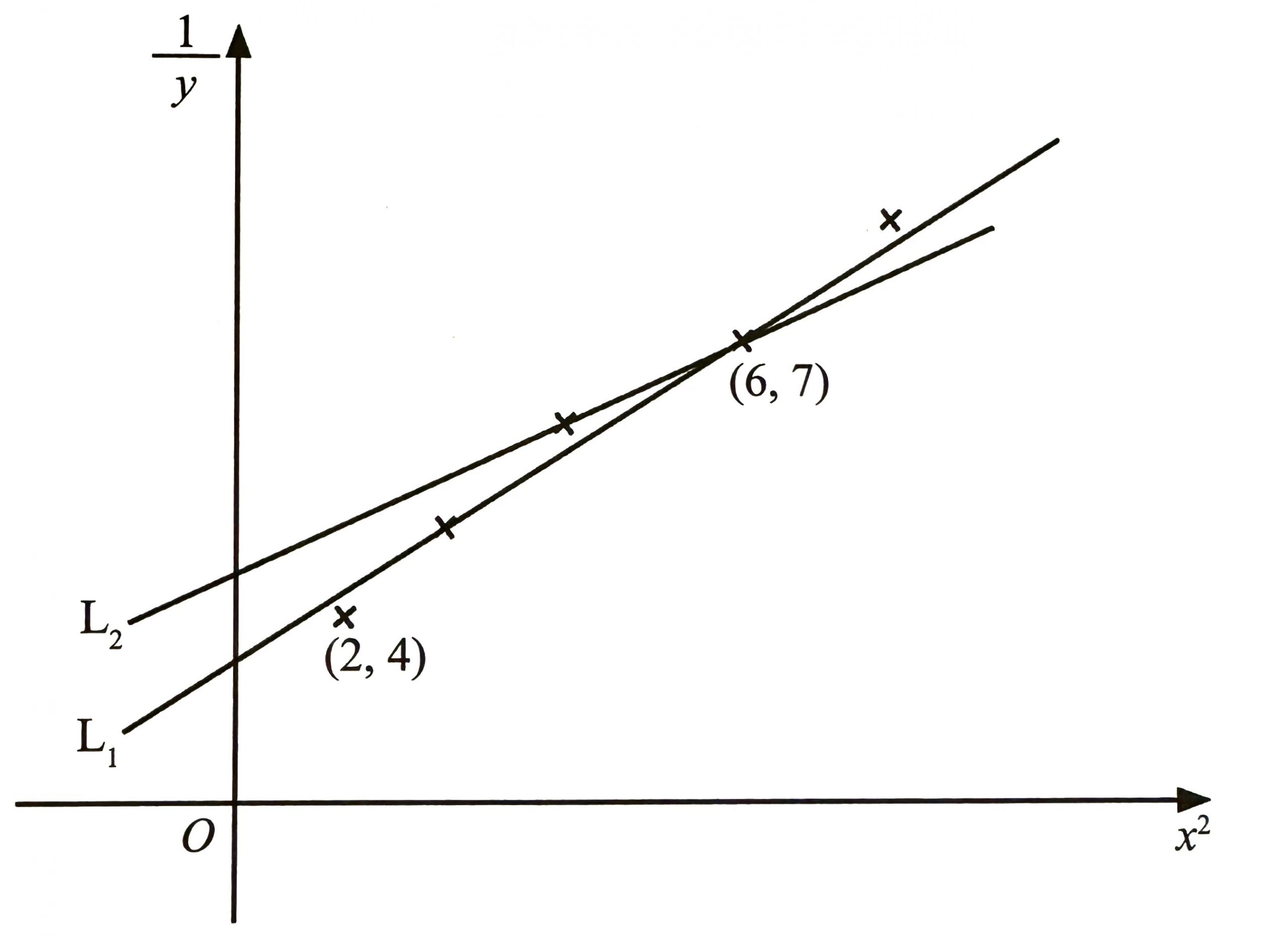
(a) Which straight line is a suitable line of best fit? Give a reason for your answer.
[1 mark]
(b) Given that (10, 9) lies on the line of best fit, express y in terms of x.
[3 marks]
Solution:
(a)
L1 is suitable because it passes through as many points as possible and there is equal number of points on both sides of the straight line.
(b)
$$ \begin{aligned} Y & =m X+C \\ \frac{1}{y} & =\frac{(7-4)}{(6-2)}\left(x^2\right)+C \\ \frac{1}{y} & =\frac{3}{4} x^2+C \end{aligned} $$
$$ \begin{aligned} & \text A t(10,9), \\ & 9=\frac{3}{4}(10)+C \\ & 9=\frac{15}{2}+C \\ & \frac{3}{2}=C \end{aligned} $$
$$ \begin{aligned} & \frac{1}{y}=\frac{3}{4} x^2+\frac{3}{2} \\ & \frac{1}{y}=\frac{3 x^2+6}{4} \\ & \frac{y}{1}=\frac{4}{3 x^2+6} \\ & y=\frac{3}{4 x^2+6} \end{aligned} $$
$$ \text { Diagram } 2 \text { shows two straight lines, } \mathrm{L}_1 \text { and } \mathrm{L}_2 \text {, drawn based on five plotted points on a plane } \frac{1}{y} \text { against } x^2 \text {. } $$

(a) Which straight line is a suitable line of best fit? Give a reason for your answer.
[1 mark]
(b) Given that (10, 9) lies on the line of best fit, express y in terms of x.
[3 marks]
Solution:
(a)
L1 is suitable because it passes through as many points as possible and there is equal number of points on both sides of the straight line.
(b)
$$ \begin{aligned} Y & =m X+C \\ \frac{1}{y} & =\frac{(7-4)}{(6-2)}\left(x^2\right)+C \\ \frac{1}{y} & =\frac{3}{4} x^2+C \end{aligned} $$
$$ \begin{aligned} & \text A t(10,9), \\ & 9=\frac{3}{4}(10)+C \\ & 9=\frac{15}{2}+C \\ & \frac{3}{2}=C \end{aligned} $$
$$ \begin{aligned} & \frac{1}{y}=\frac{3}{4} x^2+\frac{3}{2} \\ & \frac{1}{y}=\frac{3 x^2+6}{4} \\ & \frac{y}{1}=\frac{4}{3 x^2+6} \\ & y=\frac{3}{4 x^2+6} \end{aligned} $$