Question 6:
Diagram 5 shows two curves are intersecting at point A. The straight line AB is parallel to the x-axis.
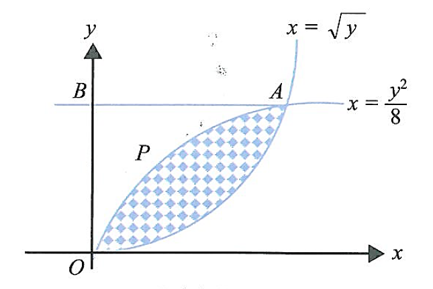
Find
(a) the equation of the straight line AB, [2 marks]
(b) area, in unit2, of the shaded region, [3 marks]
(c) the volume generated, in term of π, when the region P, which bounded by the curve , the straight line AB and the y-axis, is revolved 360∘ about the y-axis. [3 marks]
Solution:
(a)
(b)
(c)
Diagram 5 shows two curves are intersecting at point A. The straight line AB is parallel to the x-axis.

Find
(a) the equation of the straight line AB, [2 marks]
(b) area, in unit2, of the shaded region, [3 marks]
(c) the volume generated, in term of π, when the region P, which bounded by the curve , the straight line AB and the y-axis, is revolved 360∘ about the y-axis. [3 marks]
Solution:
(a)
(b)
(c)