SPM 2021 Add Maths Trial Paper (Selangor) – Paper 2 (Question 5)

Question 5:
Diagram 4(a) shows two concentric circles with the centre O. ABC is a tangent to the smaller circle at B. Five triangles OAC form a regular pentagon inscribed the bigger circle as in Diagram 4(b).


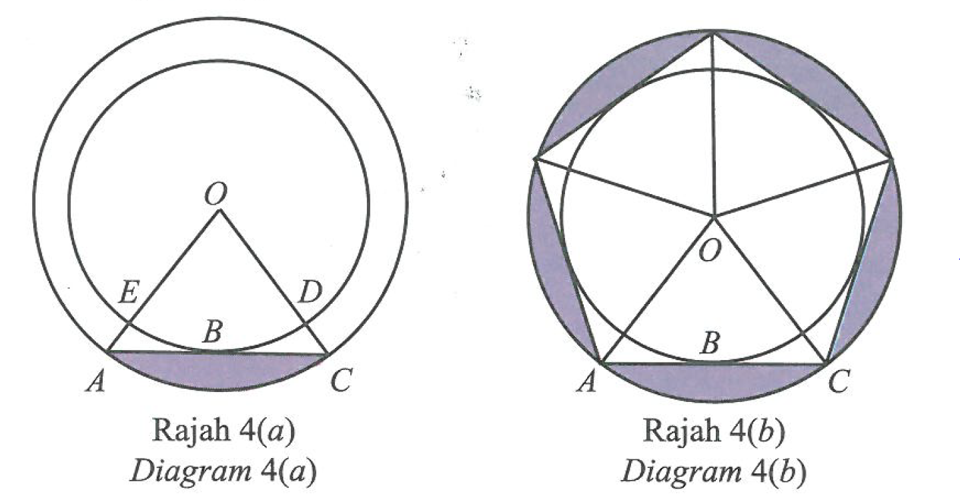
By using π = 3.142,
(a) show that the length of OA = 9.889 cm, given that OD = 8 cm. [1 mark]

(b) calculate
(i) the difference between the length, in cm, of arc AC and arc⁡ DE.
(ii) the area, in cm², of the blue coloured region in Diagram 4(b).
[6 marks]


Solution:
(a)

$\begin{array}{l}\text{From diagram 4}\left(b\right),\\ \angle AOC=\frac{{360}^o}{5}={72}^o\\ \\ \text{From diagram 4}\left(a\right),\\ OD=OB=8\text{ cm}\\ \angle AOB=\frac{1}{2}\left({72}^o\right)={36}^o\\ \cos \angle AOB=\frac{OB}{OA}\\ \cos {36}^o=\frac{8}{OA}\\ OA=\frac{8}{\cos {36}^o}\\ OA=9.889\text{ cm (shown)}\end{array}$


(b)(i)

$\begin{array}{l}\angle AOC={72}^o\times \frac{\pi }{{180}^o}=\frac{2}{5}\pi \text{ rad}\\ \\ \text{Difference of arc }AC\text{ and arc }DE\\ =r_1\theta -r_2\theta \\ =\left(9.889\right)\left(\frac{2}{5}\pi \right)-\left(8\right)\left(\frac{2}{5}\pi \right)\\ =2.374\text{ cm}\end{array}$


(b)(ii)

$\begin{array}{l}\text{Blue coloured region in Diagram 4}\left(b\right)\\ =\text{ area of circle}-\text{ area of 5 triangles}\\ =\pi r^2-5\left(\frac{1}{2}{r}^2\sin \theta \right)\\ =\pi {\left(9.889\right)}^2-5\left[\frac{1}{2}{\left(9.889\right)}^2\sin {72}^o\right]\\ =307.224-232.515\\ =74.709{\text{ cm}}^2\end{array}$