Question 20:
Find the range of values of k if the quadratic equation 3(x2 – kx – 1) = k – k2 has two real and distinc roots.
Solution:

Find the range of values of k if the quadratic equation 3(x2 – kx – 1) = k – k2 has two real and distinc roots.
Solution:

Question 21:
Given that the quadratic equation hx2 – (h + 2)x – (h – 4) = 0 has real and distinc roots. Find the range of values of h.
Solution:

Given that the quadratic equation hx2 – (h + 2)x – (h – 4) = 0 has real and distinc roots. Find the range of values of h.
Solution:

Question 22:
The diagram below shows the graph of the quadratic function f(x) = (x + 3)2 + 2h – 6, where h is a constant.
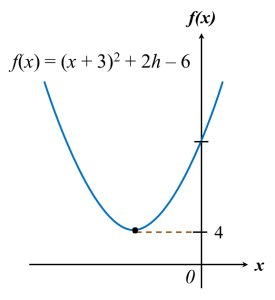
(a) State the equation of the axis of symmetry of the curve.
(b) Given the minimum value of the function is 4, find the value of h.
Solution:
(a)
When x + 3 = 0
x = –3
Therefore, equation of the axis of symmetry of the curve is x = –3.
(b)
When x + 3 = 0, f(x) = 2h – 6
Minimum value of f(x) is 2h – 6.
2h – 6 = 4
2h = 10
h = 5
The diagram below shows the graph of the quadratic function f(x) = (x + 3)2 + 2h – 6, where h is a constant.

(a) State the equation of the axis of symmetry of the curve.
(b) Given the minimum value of the function is 4, find the value of h.
Solution:
(a)
When x + 3 = 0
x = –3
Therefore, equation of the axis of symmetry of the curve is x = –3.
(b)
When x + 3 = 0, f(x) = 2h – 6
Minimum value of f(x) is 2h – 6.
2h – 6 = 4
2h = 10
h = 5