Question 4:
Diagram 2 shows the triangle ABC, AR is parallel to PQ.
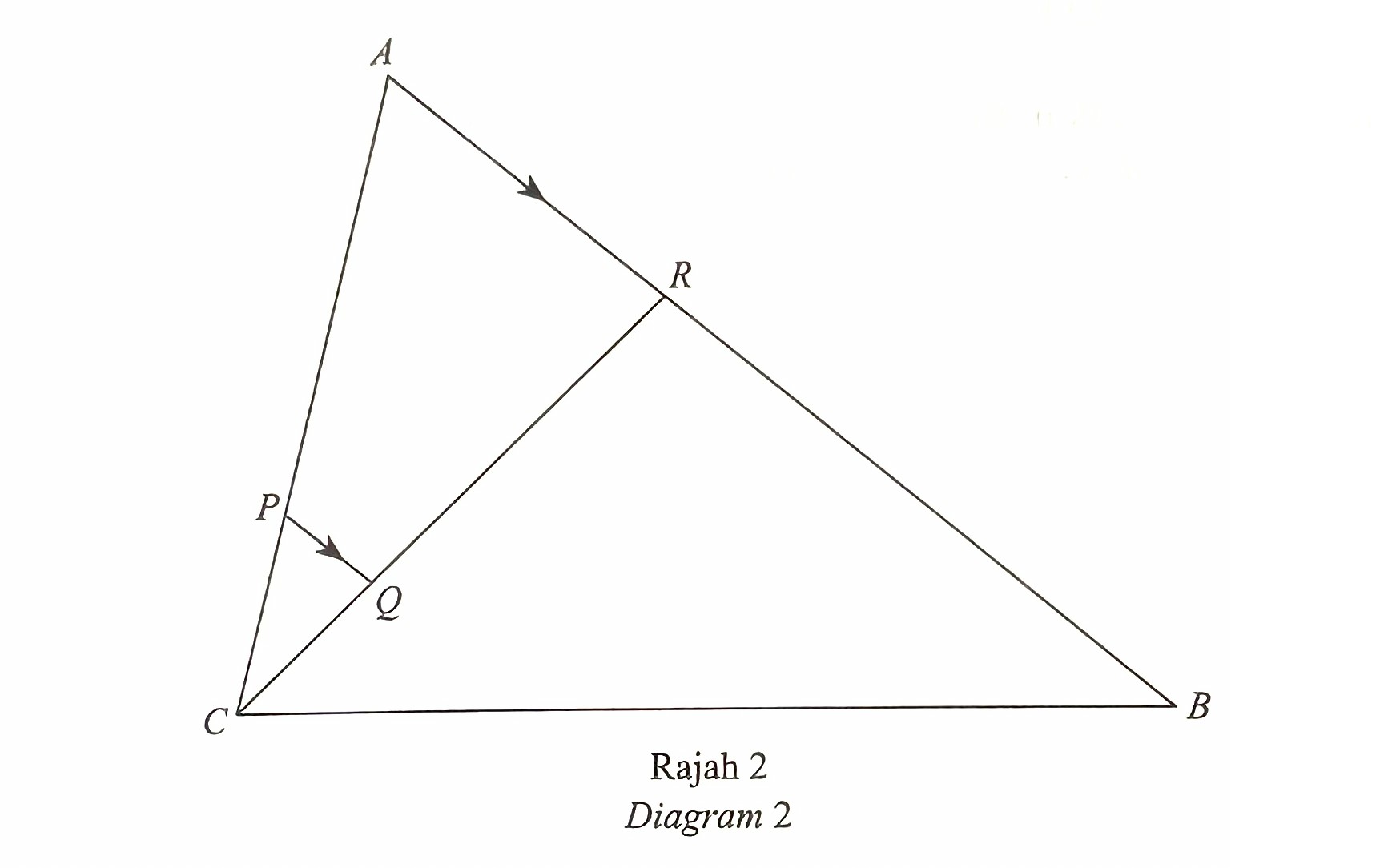
$$ \text { It is given that } \overrightarrow{C B}=6 \underline{u}, \overrightarrow{C A}=5 \underline{v} \text { and } \overrightarrow{A R}=\frac{2}{5} \overrightarrow{A B} \text {. } $$
$$ \text { (a) Express in terms of } \underline{u} \text { and } \underline{v} \text { : } $$
$$ \text { (i) } \overrightarrow{A B} \text {, } $$
$$ \text { (ii) } \overrightarrow{C R} \text {. } $$
[3 marks]
(b)(i)
$$ \text { Given that } \underline{u}=5 \underline{i} \text { and } \underline{v}=\underline{i}+4 \underline{j} \text {, find }|\overrightarrow{C R}| \text {. } $$
(b)(ii)
Hence, find the shortest distance from point A to the straight line CR if the area of Δ CPQ is 40/3 unit2 and CQ : QR = 1 : 2.
[5 marks]
Answer:
(a)(i)
$$ \begin{aligned} \overrightarrow{A B} & =\overrightarrow{A C}+\overrightarrow{C B} \\ & =-5 \underline{v}+6 \underline{u} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} \overrightarrow{C R} & =\overrightarrow{C A}+\overrightarrow{A R} \\ & =5 \underline{v}+\frac{2}{5} \overrightarrow{A B} \\ & =5 \underline{v}+\frac{2}{5}(-5 \underline{v}+6 \underline{u}) \\ & =5 \underline{v}-2 \underline{v}+\frac{12}{5} \underline{u} \\ & =3 \underline{v}+\frac{12}{5} \underline{u} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & \overrightarrow{C R}=3(\underline{i}+4 \underline{j})+\frac{12}{5}(5 \underline{i}) \\ & \overrightarrow{C R}=3 \underline{i}+12 \underline{j}+12 \underline{i} \\ & \overrightarrow{C R}=15 \underline{i}+12 \underline{j} \\ & |\overrightarrow{C R}|=\sqrt{15^2+12^2} \\ & |\overrightarrow{C R}|=3 \sqrt{41} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} &\begin{aligned} \text { Area, } \triangle C A R & =3 \times \triangle C P Q \\ \frac{1}{2} \times C R \times \text { height } & =3\left(\frac{40}{3}\right) \\ \frac{1}{2} \times 3 \sqrt{41} \times x & =40 \\ 3 \sqrt{41} \times x & =80 \\ x & =\frac{80}{3 \sqrt{41}} \\ x & =\frac{80}{3 \sqrt{41}} \times \frac{3 \sqrt{41}}{3 \sqrt{41}} \\ x & =\frac{80 \sqrt{41}}{123} \end{aligned}\\ &\therefore \text { Shortest distance }=4.1646 \text { unit } \end{aligned} $$
Diagram 2 shows the triangle ABC, AR is parallel to PQ.

$$ \text { It is given that } \overrightarrow{C B}=6 \underline{u}, \overrightarrow{C A}=5 \underline{v} \text { and } \overrightarrow{A R}=\frac{2}{5} \overrightarrow{A B} \text {. } $$
$$ \text { (a) Express in terms of } \underline{u} \text { and } \underline{v} \text { : } $$
$$ \text { (i) } \overrightarrow{A B} \text {, } $$
$$ \text { (ii) } \overrightarrow{C R} \text {. } $$
[3 marks]
(b)(i)
$$ \text { Given that } \underline{u}=5 \underline{i} \text { and } \underline{v}=\underline{i}+4 \underline{j} \text {, find }|\overrightarrow{C R}| \text {. } $$
(b)(ii)
Hence, find the shortest distance from point A to the straight line CR if the area of Δ CPQ is 40/3 unit2 and CQ : QR = 1 : 2.
[5 marks]
Answer:
(a)(i)
$$ \begin{aligned} \overrightarrow{A B} & =\overrightarrow{A C}+\overrightarrow{C B} \\ & =-5 \underline{v}+6 \underline{u} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} \overrightarrow{C R} & =\overrightarrow{C A}+\overrightarrow{A R} \\ & =5 \underline{v}+\frac{2}{5} \overrightarrow{A B} \\ & =5 \underline{v}+\frac{2}{5}(-5 \underline{v}+6 \underline{u}) \\ & =5 \underline{v}-2 \underline{v}+\frac{12}{5} \underline{u} \\ & =3 \underline{v}+\frac{12}{5} \underline{u} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & \overrightarrow{C R}=3(\underline{i}+4 \underline{j})+\frac{12}{5}(5 \underline{i}) \\ & \overrightarrow{C R}=3 \underline{i}+12 \underline{j}+12 \underline{i} \\ & \overrightarrow{C R}=15 \underline{i}+12 \underline{j} \\ & |\overrightarrow{C R}|=\sqrt{15^2+12^2} \\ & |\overrightarrow{C R}|=3 \sqrt{41} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} &\begin{aligned} \text { Area, } \triangle C A R & =3 \times \triangle C P Q \\ \frac{1}{2} \times C R \times \text { height } & =3\left(\frac{40}{3}\right) \\ \frac{1}{2} \times 3 \sqrt{41} \times x & =40 \\ 3 \sqrt{41} \times x & =80 \\ x & =\frac{80}{3 \sqrt{41}} \\ x & =\frac{80}{3 \sqrt{41}} \times \frac{3 \sqrt{41}}{3 \sqrt{41}} \\ x & =\frac{80 \sqrt{41}}{123} \end{aligned}\\ &\therefore \text { Shortest distance }=4.1646 \text { unit } \end{aligned} $$
Question 5:
A curve has a gradient function, dy/dx = 4x – 6 and passes through P(1, 4).
(a) Find the equation of the curve. [3 marks]
(b) The normal to the curve at point P intersects the curve again at point Q. Find the coordinates of Q. [4 marks]
Answer:
(a)
$$ \begin{aligned} & y=\int(4 x-6) \mathrm{d} x \\ & y=\frac{4 x^2}{2}-6 x+c \\ & y=2 x^2-6 x+c, \text { } \text { pass through }(1,4) \\ & 4=2(1)^2-(6) 1+c \\ & 4=-4+c \\ & c=4+4 \\ & c=8 \\ & \therefore y=2 x^2-6 x+8 \end{aligned} $$
(b)
$$ \begin{aligned} & m_{\text { } \text { tangent }}: \frac{\mathrm{d} y}{\mathrm{~d} x}=4 x-6 \text { } \text { at }(1,4) \\ & \frac{\mathrm{d} y}{\mathrm{~d} x}=4(1)-6 \\ & \quad=-2 \\ & m_{\text {normal }} \times m_{\text { } \text { tangent }}=-1 \\ & \quad m_{\text {normal }} \times-2=-1 \\ & \quad m_{\text {normal }}=\frac{1}{2} \end{aligned} $$ Equation of normal passes through P(1, 4) : $$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-4 & =\frac{1}{2}(x-1) \\ y & =\frac{1}{2} x-\frac{1}{2}+4 \end{aligned} $$
$$ \begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ y= & 2 x^2-6 x+8 \ldots \text { (1) } \\ y= & \frac{1}{2} x+\frac{7}{2} \ldots \text { (2) } \end{aligned} $$
$$ \begin{aligned} &\text { (1) }=\text { (2) ; }\\ &\begin{aligned} 2 x^2-6 x+8 & =\frac{1}{2} x+\frac{7}{2} \\ 2 x^2-6 x-\frac{1}{2} x+8-\frac{7}{2} & =0 \\ 2 x^2-\frac{13}{2} x+\frac{9}{2} & =0 \\ 4 x^2-13 x+9 & =0 \\ (4 x-9)(x-1) & =0 \\ 4 x-9=0, x-1=0 & \\ x=\frac{9}{4}, & x=1 \text { ( ignore) } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { From (2), }\\ &\begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ & y=\frac{1}{2}\left(\frac{9}{4}\right)+\frac{7}{2} \\ & y=\frac{37}{8} \\ & \therefore Q\left(\frac{9}{4}, \frac{37}{8}\right) \end{aligned} \end{aligned} $$
A curve has a gradient function, dy/dx = 4x – 6 and passes through P(1, 4).
(a) Find the equation of the curve. [3 marks]
(b) The normal to the curve at point P intersects the curve again at point Q. Find the coordinates of Q. [4 marks]
Answer:
(a)
$$ \begin{aligned} & y=\int(4 x-6) \mathrm{d} x \\ & y=\frac{4 x^2}{2}-6 x+c \\ & y=2 x^2-6 x+c, \text { } \text { pass through }(1,4) \\ & 4=2(1)^2-(6) 1+c \\ & 4=-4+c \\ & c=4+4 \\ & c=8 \\ & \therefore y=2 x^2-6 x+8 \end{aligned} $$
(b)
$$ \begin{aligned} & m_{\text { } \text { tangent }}: \frac{\mathrm{d} y}{\mathrm{~d} x}=4 x-6 \text { } \text { at }(1,4) \\ & \frac{\mathrm{d} y}{\mathrm{~d} x}=4(1)-6 \\ & \quad=-2 \\ & m_{\text {normal }} \times m_{\text { } \text { tangent }}=-1 \\ & \quad m_{\text {normal }} \times-2=-1 \\ & \quad m_{\text {normal }}=\frac{1}{2} \end{aligned} $$ Equation of normal passes through P(1, 4) : $$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-4 & =\frac{1}{2}(x-1) \\ y & =\frac{1}{2} x-\frac{1}{2}+4 \end{aligned} $$
$$ \begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ y= & 2 x^2-6 x+8 \ldots \text { (1) } \\ y= & \frac{1}{2} x+\frac{7}{2} \ldots \text { (2) } \end{aligned} $$
$$ \begin{aligned} &\text { (1) }=\text { (2) ; }\\ &\begin{aligned} 2 x^2-6 x+8 & =\frac{1}{2} x+\frac{7}{2} \\ 2 x^2-6 x-\frac{1}{2} x+8-\frac{7}{2} & =0 \\ 2 x^2-\frac{13}{2} x+\frac{9}{2} & =0 \\ 4 x^2-13 x+9 & =0 \\ (4 x-9)(x-1) & =0 \\ 4 x-9=0, x-1=0 & \\ x=\frac{9}{4}, & x=1 \text { ( ignore) } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { From (2), }\\ &\begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ & y=\frac{1}{2}\left(\frac{9}{4}\right)+\frac{7}{2} \\ & y=\frac{37}{8} \\ & \therefore Q\left(\frac{9}{4}, \frac{37}{8}\right) \end{aligned} \end{aligned} $$