Question 6:
Table 1 shows the categories for body mass index of a group of male workers in a company. The body mass index is normally distributed.

It is given that 44% of the workers are categorised as either underweight or normal weight while 12% were categorised as obese. It is found that, 1 out of n workers were in the underweight category.
Find the value of n.
[6 marks]
Answer:
$$ \begin{aligned} P(x<25) & =44 \% \\ P\left(Z<\frac{25-\mu}{\sigma}\right) & =0.44 \\ \frac{25-\mu}{\sigma} & =-0.151 \\ 25-\mu & =-0.151 \sigma \ldots(1) \end{aligned} $$
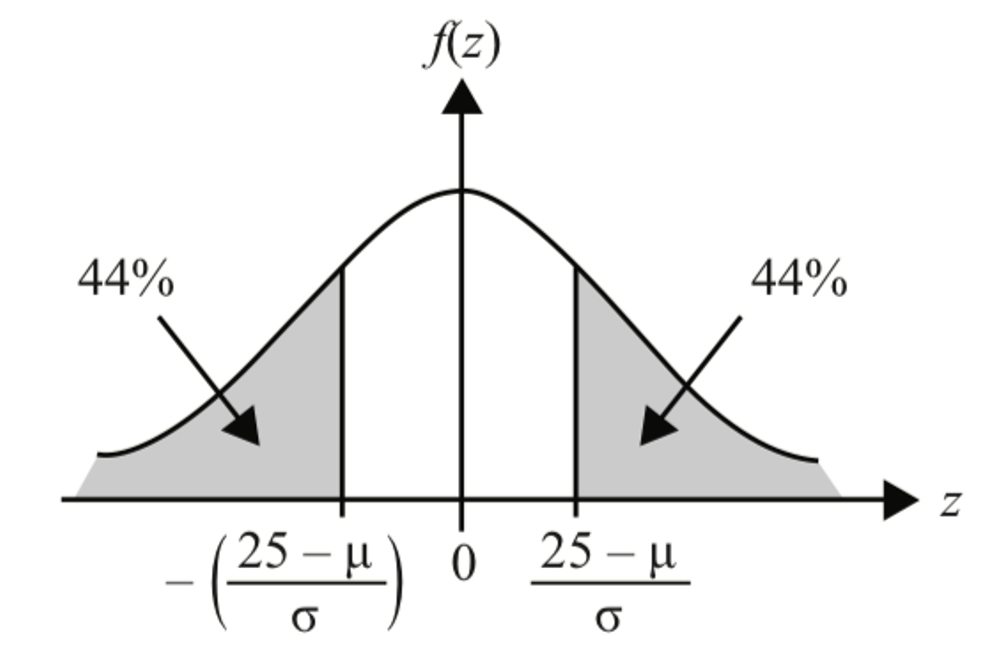
$$ \begin{aligned} P(x \geqslant 30) & =12 \% \\ P\left(Z>\frac{30-\mu}{\sigma}\right) & =0.12 \\ \frac{30-\mu}{\sigma} & =1.175 \\ 30-\mu & =1.175 \sigma \ldots(2) \end{aligned} $$
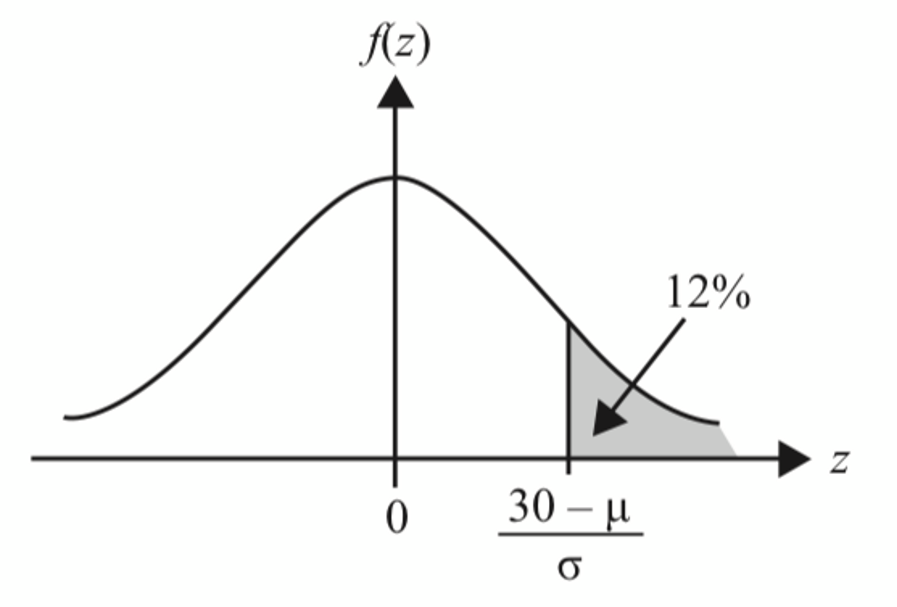
$$ \begin{aligned} &\text { (2) – (1); }\\ &\begin{aligned} (30-\mu)-(25-\mu) & =1.175 \sigma-(-0.151 \sigma) \\ 30-\mu-25+\mu & =1.175 \sigma+0.151 \sigma \\ 5 & =1.326 \sigma \\ \frac{5}{1.326} & =\sigma \\ \sigma & =3.7707 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { From (1), }\\ &\begin{aligned} 25-\mu & =-0.151 \sigma \\ 25-\mu & =-0.151(3.7707) \\ -\mu & =-0.5694-25 \\ -\mu & =-25.5694 \\ \mu & =25.5694 \end{aligned} \end{aligned} $$
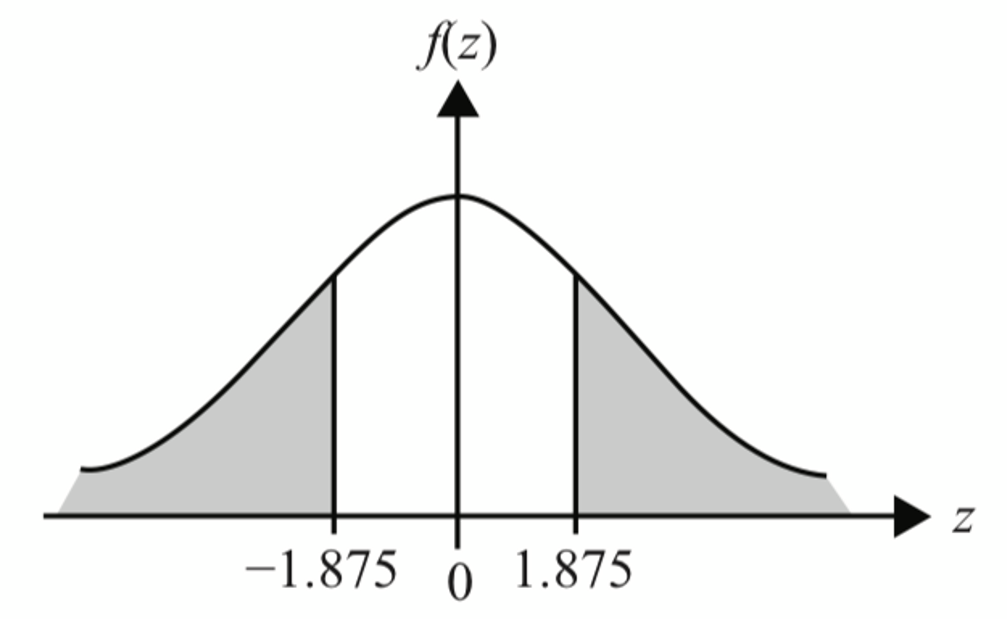
$$ \begin{aligned} P(X<18.5) & =\frac{1}{n} \\ P\left(Z<\frac{18.5-25.57}{3.77}\right) & =\frac{1}{n} \\ P(Z<-1.875) & =\frac{1}{n} \\ 0.0303 & =\frac{1}{n} \\ n & =\frac{1}{0.0303} \\ n & =33 \end{aligned} $$
Table 1 shows the categories for body mass index of a group of male workers in a company. The body mass index is normally distributed.

It is given that 44% of the workers are categorised as either underweight or normal weight while 12% were categorised as obese. It is found that, 1 out of n workers were in the underweight category.
Find the value of n.
[6 marks]
Answer:
$$ \begin{aligned} P(x<25) & =44 \% \\ P\left(Z<\frac{25-\mu}{\sigma}\right) & =0.44 \\ \frac{25-\mu}{\sigma} & =-0.151 \\ 25-\mu & =-0.151 \sigma \ldots(1) \end{aligned} $$

$$ \begin{aligned} P(x \geqslant 30) & =12 \% \\ P\left(Z>\frac{30-\mu}{\sigma}\right) & =0.12 \\ \frac{30-\mu}{\sigma} & =1.175 \\ 30-\mu & =1.175 \sigma \ldots(2) \end{aligned} $$

$$ \begin{aligned} &\text { (2) – (1); }\\ &\begin{aligned} (30-\mu)-(25-\mu) & =1.175 \sigma-(-0.151 \sigma) \\ 30-\mu-25+\mu & =1.175 \sigma+0.151 \sigma \\ 5 & =1.326 \sigma \\ \frac{5}{1.326} & =\sigma \\ \sigma & =3.7707 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { From (1), }\\ &\begin{aligned} 25-\mu & =-0.151 \sigma \\ 25-\mu & =-0.151(3.7707) \\ -\mu & =-0.5694-25 \\ -\mu & =-25.5694 \\ \mu & =25.5694 \end{aligned} \end{aligned} $$

$$ \begin{aligned} P(X<18.5) & =\frac{1}{n} \\ P\left(Z<\frac{18.5-25.57}{3.77}\right) & =\frac{1}{n} \\ P(Z<-1.875) & =\frac{1}{n} \\ 0.0303 & =\frac{1}{n} \\ n & =\frac{1}{0.0303} \\ n & =33 \end{aligned} $$