Question 7:
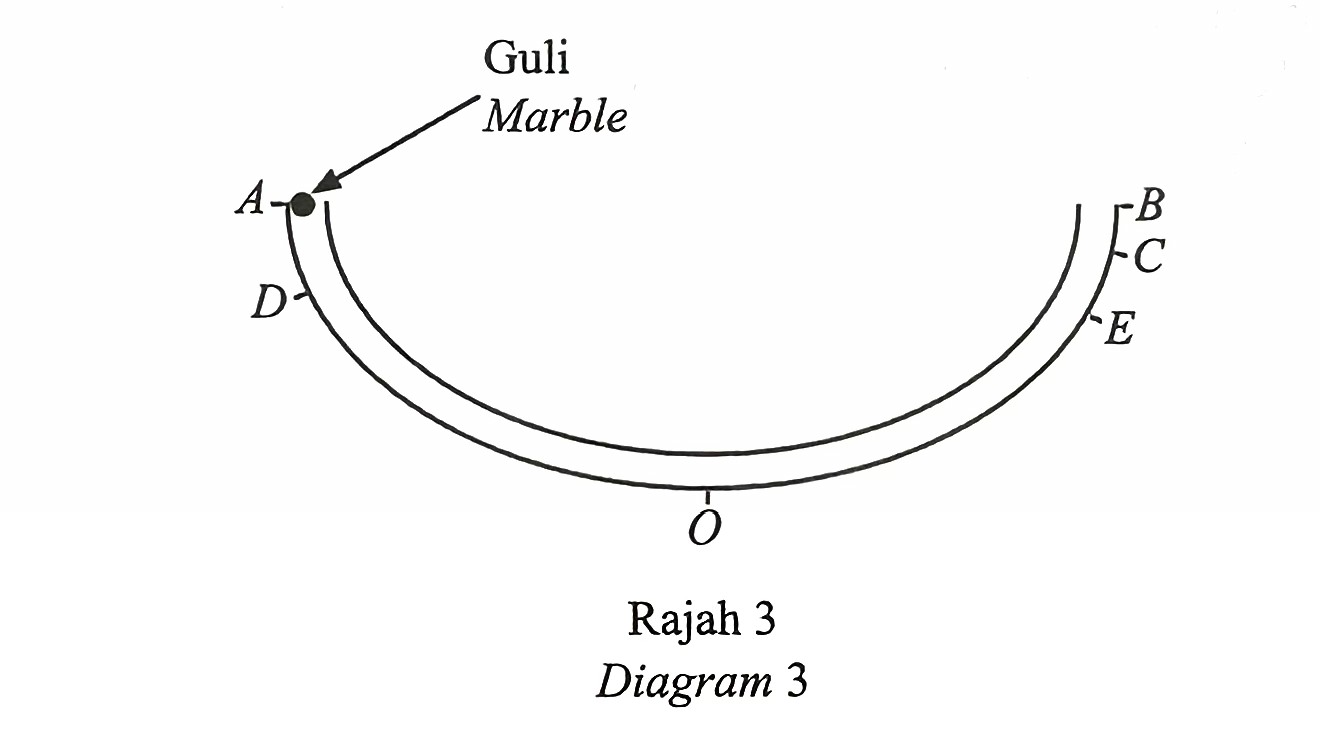
Diagram 3 shows a symmetrical tube such that points A and B are on the same level.
A marble is released from point A and moves through the tube towards point B until it stops instantaneously for the first time at point C.
The marble will move back and forth through the tube until it stops completely at point O.
The marble stops instantaneously for the second time at point D and stops instantaneously for the third time at point E.
The distance travelled by the marble from point A to point C, point C to point D and subsequent distances are in the same ratio.
The total distance travelled by the marble from point A to point C and then from point C to point D is 629/4 cm. The distance travelled from point D to point E is 4913/80 cm.
If the marble takes 1 minute to stop completely at point O, determine whether the average speed of the marble exceeds 10 cm s-1 or not. Show your calculation.
[10 marks]
Answer:
The distance travelled are in the same ratio → Geometric progression
$$ \begin{aligned} & T_1: A \rightarrow C \\ & T_2: C \rightarrow D \\ & T_3: D \rightarrow E \end{aligned} $$
$$ \begin{gathered} T_1+T_2=\frac{629}{4} \\ a+a r^{2-1}=\frac{629}{4} \\ a+a r=\frac{629}{4} \\ a(1+r)=\frac{629}{4} \ldots \text { (1) } \\ T_3=\frac{4913}{80} \\ a r^{3-1}=\frac{4913}{80} \\ a r^2=\frac{4913}{80} \ldots \text { (2) } \end{gathered} $$
$$ \frac{(2)}{(1)} ; \quad \frac{a r^2}{a(1+r)}=\frac{\left(\frac{4913}{80}\right)}{\left(\frac{629}{4}\right)} $$
$$ \begin{aligned} \frac{r^2}{1+r} & =\frac{289}{740} & \\ 740 r^2 & =289+289 r & \\ 740 r^2-289 r-289 & =0 & \\ (20 r-17)(37 r+17) & =0 & \\ 20 r-17=0 \quad, \quad 37 r+17 & =0 & \\ r=\frac{17}{20} \quad ; \quad r & =-\frac{17}{37}(\text { ignore } ) & \end{aligned} $$
$$ \begin{aligned} &\text { From (1), }\\ &\begin{aligned} a(1+r) & =\frac{629}{4} \\ a\left(1+\frac{17}{20}\right) & =\frac{629}{4} \\ \frac{37}{20} a & =\frac{629}{4} \\ a & =\frac{\left(\frac{629}{4}\right)}{\left(\frac{37}{20}\right)} \\ a & =85 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Total distance } & =S_{\infty} \\ & =\frac{85}{1-\frac{17}{20}} \\ & =566 \frac{2}{3} \mathrm{~cm} \\ \text { Average speed } & =\frac{566 \frac{2}{3} \mathrm{~cm}}{60 \mathrm{~s}} \\ & =9.44 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
$$ 9.44 \mathrm{~cm} \mathrm{~s}^{-1}<10 \mathrm{~cm} \mathrm{~s}^{-1} $$
The average speed of the marble does not exceed 10 cm s-1.
Diagram 3 shows a symmetrical tube such that points A and B are on the same level.
A marble is released from point A and moves through the tube towards point B until it stops instantaneously for the first time at point C.
The marble will move back and forth through the tube until it stops completely at point O.
The marble stops instantaneously for the second time at point D and stops instantaneously for the third time at point E.
The distance travelled by the marble from point A to point C, point C to point D and subsequent distances are in the same ratio.

The total distance travelled by the marble from point A to point C and then from point C to point D is 629/4 cm. The distance travelled from point D to point E is 4913/80 cm.
If the marble takes 1 minute to stop completely at point O, determine whether the average speed of the marble exceeds 10 cm s-1 or not. Show your calculation.
[10 marks]
Answer:
The distance travelled are in the same ratio → Geometric progression
$$ \begin{aligned} & T_1: A \rightarrow C \\ & T_2: C \rightarrow D \\ & T_3: D \rightarrow E \end{aligned} $$
$$ \begin{gathered} T_1+T_2=\frac{629}{4} \\ a+a r^{2-1}=\frac{629}{4} \\ a+a r=\frac{629}{4} \\ a(1+r)=\frac{629}{4} \ldots \text { (1) } \\ T_3=\frac{4913}{80} \\ a r^{3-1}=\frac{4913}{80} \\ a r^2=\frac{4913}{80} \ldots \text { (2) } \end{gathered} $$
$$ \frac{(2)}{(1)} ; \quad \frac{a r^2}{a(1+r)}=\frac{\left(\frac{4913}{80}\right)}{\left(\frac{629}{4}\right)} $$
$$ \begin{aligned} \frac{r^2}{1+r} & =\frac{289}{740} & \\ 740 r^2 & =289+289 r & \\ 740 r^2-289 r-289 & =0 & \\ (20 r-17)(37 r+17) & =0 & \\ 20 r-17=0 \quad, \quad 37 r+17 & =0 & \\ r=\frac{17}{20} \quad ; \quad r & =-\frac{17}{37}(\text { ignore } ) & \end{aligned} $$
$$ \begin{aligned} &\text { From (1), }\\ &\begin{aligned} a(1+r) & =\frac{629}{4} \\ a\left(1+\frac{17}{20}\right) & =\frac{629}{4} \\ \frac{37}{20} a & =\frac{629}{4} \\ a & =\frac{\left(\frac{629}{4}\right)}{\left(\frac{37}{20}\right)} \\ a & =85 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Total distance } & =S_{\infty} \\ & =\frac{85}{1-\frac{17}{20}} \\ & =566 \frac{2}{3} \mathrm{~cm} \\ \text { Average speed } & =\frac{566 \frac{2}{3} \mathrm{~cm}}{60 \mathrm{~s}} \\ & =9.44 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
$$ 9.44 \mathrm{~cm} \mathrm{~s}^{-1}<10 \mathrm{~cm} \mathrm{~s}^{-1} $$
The average speed of the marble does not exceed 10 cm s-1.
Question 8:
(a)(i)
$$ \text { Prove that cos } 2 \theta=\operatorname{cos}^2 \theta-\sin ^2 \theta \text {. } $$
(a)(ii)
$$ \text { Hence, solve the equation } 3 \operatorname{cos}^2 \theta=2+3 \sin ^2 \theta \text { for } 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \text {. } $$
[5 marks]
(b)(i)
$$ \text { Sketch the graph } y=-\left|\operatorname{cos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \text { for } 0 \leqslant \theta \leqslant 2 \pi \text {. } $$
(b)(ii)
There are 8 solutions when y = h, such that h is a constant. State the range of values of h.
[5 marks]
Answer:
(a)(i)
$$ \begin{aligned} & \mathrm{cos} \ 2 \theta=\mathrm{cos} \ (\theta+\theta) \\ & \mathrm{cos} \ 2 \theta=\mathrm{cos} \ \theta \mathrm{cos} \theta-\sin \theta \sin \theta \\ & \mathrm{cos} \ 2 \theta=\mathrm{cos}^2 \ \theta-\sin ^2 \theta(\text { Proven } ) \end{aligned} $$
(a)(ii)
$$ \begin{aligned} &\begin{aligned} 3 \mathrm{cos}^2 \ \theta & =2+3 \sin ^2 \theta \\ 3 \mathrm{cos}^2 \ \theta-3 \sin ^2 \theta & =2 \\ 3\left(\mathrm{cos}^2 \ \theta-\sin ^2 \theta\right) & =2 \\ 3 \mathrm{cos} \ 2 \theta & =2 \\ \mathrm{cos} \ 2 \theta & =\frac{2}{3}(\mathrm{I}, \mathrm{IV}) \end{aligned}\\ &\text { Reference angle: }\\ &\mathrm{cos}^{-1 } \left(\frac{2}{3}\right)=48.19^{\circ} \quad ; \quad \begin{aligned} & 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \\ & 360^{\circ} \leqslant 2 \theta \leqslant 720^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} 2 \theta & =48.19^{\circ}, 360^{\circ}-48.19^{\circ}, 360^{\circ}+48.19^{\circ}, 360^{\circ}+311.81^{\circ} \\ & =48.19^{\circ}, 311.81^{\circ}, 408.19^{\circ}, 671.81^{\circ} \\ \theta & =24.10^{\circ}, 155.91^{\circ}, 204.10^{\circ}, 335.91^{\circ} \\ \therefore \theta & =204.10^{\circ}, 335.91^{\circ} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & y=-\left|\mathrm{cos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \\ & y=-|\mathrm{cos} \ 2 \theta|+\frac{4}{5}, 0 \leqslant \theta \leqslant 2 \pi \end{aligned} $$
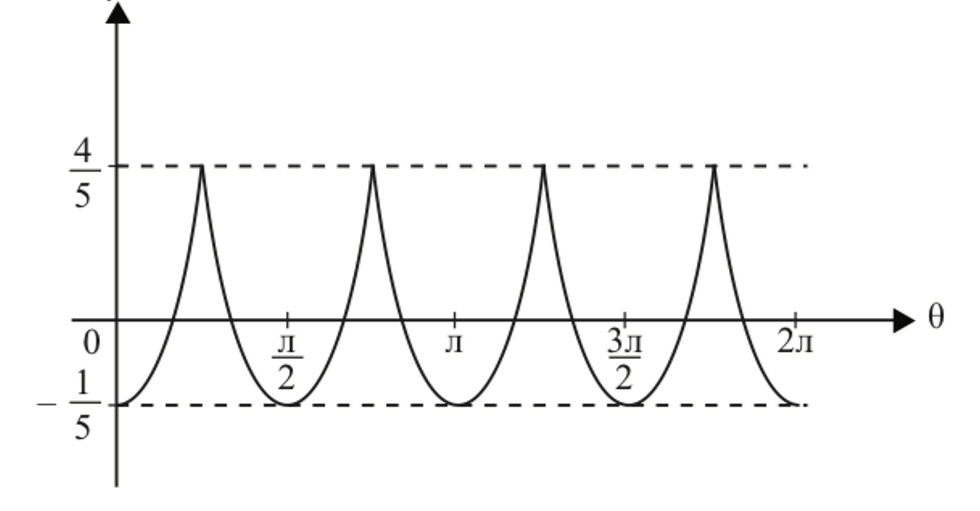
(b)(ii)
$$ -\frac{1}{5}<h<\frac{4}{5} $$
(a)(i)
$$ \text { Prove that cos } 2 \theta=\operatorname{cos}^2 \theta-\sin ^2 \theta \text {. } $$
(a)(ii)
$$ \text { Hence, solve the equation } 3 \operatorname{cos}^2 \theta=2+3 \sin ^2 \theta \text { for } 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \text {. } $$
[5 marks]
(b)(i)
$$ \text { Sketch the graph } y=-\left|\operatorname{cos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \text { for } 0 \leqslant \theta \leqslant 2 \pi \text {. } $$
(b)(ii)
There are 8 solutions when y = h, such that h is a constant. State the range of values of h.
[5 marks]
Answer:
(a)(i)
$$ \begin{aligned} & \mathrm{cos} \ 2 \theta=\mathrm{cos} \ (\theta+\theta) \\ & \mathrm{cos} \ 2 \theta=\mathrm{cos} \ \theta \mathrm{cos} \theta-\sin \theta \sin \theta \\ & \mathrm{cos} \ 2 \theta=\mathrm{cos}^2 \ \theta-\sin ^2 \theta(\text { Proven } ) \end{aligned} $$
(a)(ii)
$$ \begin{aligned} &\begin{aligned} 3 \mathrm{cos}^2 \ \theta & =2+3 \sin ^2 \theta \\ 3 \mathrm{cos}^2 \ \theta-3 \sin ^2 \theta & =2 \\ 3\left(\mathrm{cos}^2 \ \theta-\sin ^2 \theta\right) & =2 \\ 3 \mathrm{cos} \ 2 \theta & =2 \\ \mathrm{cos} \ 2 \theta & =\frac{2}{3}(\mathrm{I}, \mathrm{IV}) \end{aligned}\\ &\text { Reference angle: }\\ &\mathrm{cos}^{-1 } \left(\frac{2}{3}\right)=48.19^{\circ} \quad ; \quad \begin{aligned} & 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \\ & 360^{\circ} \leqslant 2 \theta \leqslant 720^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} 2 \theta & =48.19^{\circ}, 360^{\circ}-48.19^{\circ}, 360^{\circ}+48.19^{\circ}, 360^{\circ}+311.81^{\circ} \\ & =48.19^{\circ}, 311.81^{\circ}, 408.19^{\circ}, 671.81^{\circ} \\ \theta & =24.10^{\circ}, 155.91^{\circ}, 204.10^{\circ}, 335.91^{\circ} \\ \therefore \theta & =204.10^{\circ}, 335.91^{\circ} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & y=-\left|\mathrm{cos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \\ & y=-|\mathrm{cos} \ 2 \theta|+\frac{4}{5}, 0 \leqslant \theta \leqslant 2 \pi \end{aligned} $$

(b)(ii)
$$ -\frac{1}{5}<h<\frac{4}{5} $$