Question 2:
The quadratic function f(x) = 3x2 + 3px + p, such that p is a constant, has a minimum value of -1 .
(a) Using the method of completing the square, find the values of p. [4 marks]
(b) Sketch the graph of f(x) using the largest value of p from (a). [2 marks]
Answer:
(a)
$$ \begin{aligned} & f(x)=3 x^2+3 p x+p \\ & f(x)=3\left(x^2+p x+\frac{p}{3}\right) \\ & f(x)=3\left[x^2+p x+\left(\frac{p}{2}\right)^2-\left(\frac{p}{2}\right)^2+\frac{p}{3}\right] \\ & f(x)=3\left[\left(x+\frac{p}{2}\right)^2-\frac{p^2}{4}+\frac{p}{3}\right] \\ & f(x)=3\left(x+\frac{p}{2}\right)^2-\frac{3 p^2}{4}+p \end{aligned} $$
$$ \begin{aligned} &\text { Minimum value }=-1\\ &\begin{aligned} -\frac{3 p^2}{4}+p & =-1 \\ -3 p^2+4 p & =-4 \\ -3 p^2+4 p+4 & =0 \\ 3 p^2-4 p-4 & =0 \\ (3 p+2)(p-2) & =0 \\ 3 p+2=0, p-2 & =0 \\ p=-\frac{2}{3}, p=2 & \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & p=2 ; f(x)=3\left(x+\frac{2}{2}\right)^2-\frac{3(2)^2}{4}+2 \\ & f(x)=3(x+1)^2-1 \end{aligned} $$
$$ \begin{aligned} &\text { When } f(x)=0 \text {; }\\ &\begin{aligned} 3(x+1)^2-1 & =0 \\ (x+1)^2 & =\frac{1}{3} \\ x+1 & = \pm \sqrt{\frac{1}{3}} \\ x & =-1 \pm \sqrt{\frac{1}{3}} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { When } x=0 \text {; } \\ & f(x)=3(0+1)^2-1 \\ & \begin{aligned} f(x)=2 & \\ \text { When, } x+1 & =0 \\ x & =-1 \end{aligned} \end{aligned} $$
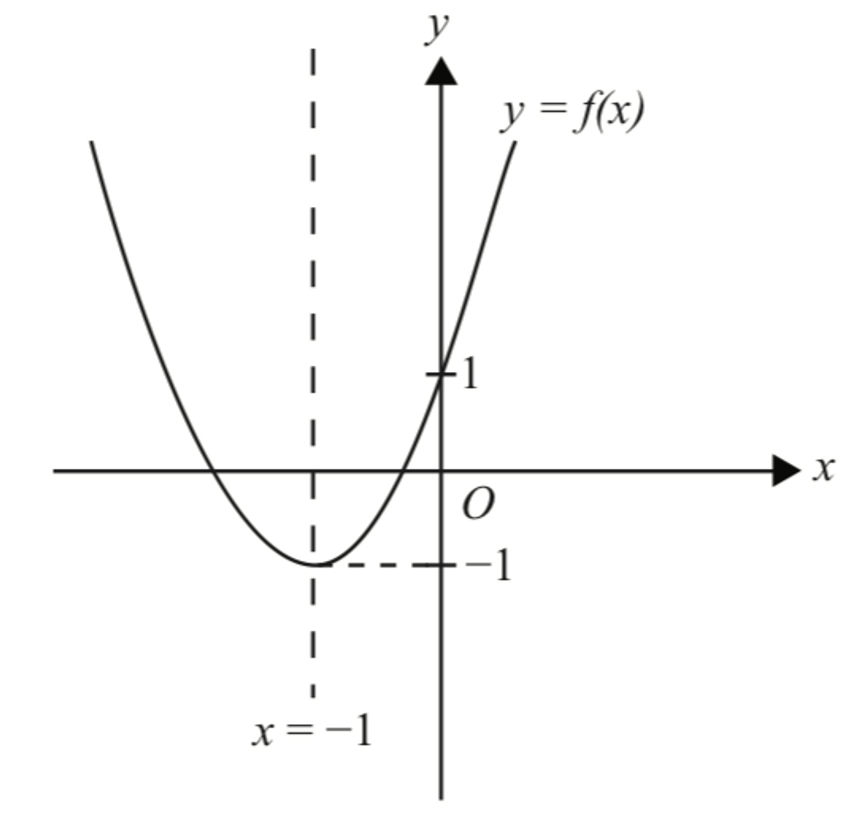
The quadratic function f(x) = 3x2 + 3px + p, such that p is a constant, has a minimum value of -1 .
(a) Using the method of completing the square, find the values of p. [4 marks]
(b) Sketch the graph of f(x) using the largest value of p from (a). [2 marks]
Answer:
(a)
$$ \begin{aligned} & f(x)=3 x^2+3 p x+p \\ & f(x)=3\left(x^2+p x+\frac{p}{3}\right) \\ & f(x)=3\left[x^2+p x+\left(\frac{p}{2}\right)^2-\left(\frac{p}{2}\right)^2+\frac{p}{3}\right] \\ & f(x)=3\left[\left(x+\frac{p}{2}\right)^2-\frac{p^2}{4}+\frac{p}{3}\right] \\ & f(x)=3\left(x+\frac{p}{2}\right)^2-\frac{3 p^2}{4}+p \end{aligned} $$
$$ \begin{aligned} &\text { Minimum value }=-1\\ &\begin{aligned} -\frac{3 p^2}{4}+p & =-1 \\ -3 p^2+4 p & =-4 \\ -3 p^2+4 p+4 & =0 \\ 3 p^2-4 p-4 & =0 \\ (3 p+2)(p-2) & =0 \\ 3 p+2=0, p-2 & =0 \\ p=-\frac{2}{3}, p=2 & \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & p=2 ; f(x)=3\left(x+\frac{2}{2}\right)^2-\frac{3(2)^2}{4}+2 \\ & f(x)=3(x+1)^2-1 \end{aligned} $$
$$ \begin{aligned} &\text { When } f(x)=0 \text {; }\\ &\begin{aligned} 3(x+1)^2-1 & =0 \\ (x+1)^2 & =\frac{1}{3} \\ x+1 & = \pm \sqrt{\frac{1}{3}} \\ x & =-1 \pm \sqrt{\frac{1}{3}} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { When } x=0 \text {; } \\ & f(x)=3(0+1)^2-1 \\ & \begin{aligned} f(x)=2 & \\ \text { When, } x+1 & =0 \\ x & =-1 \end{aligned} \end{aligned} $$

Question 3:
(a)
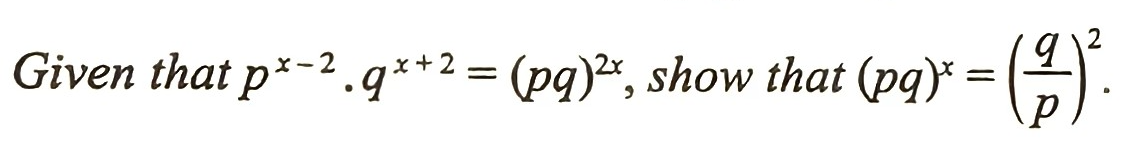
[3 marks]
(b)
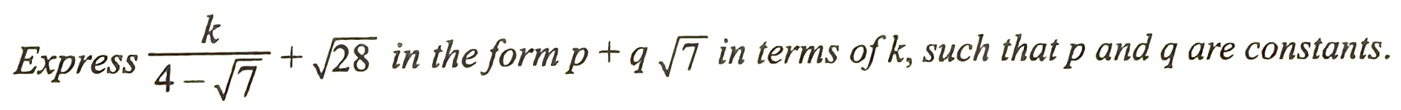
[3 marks]
Answer:
(a)
$$ \begin{aligned} p^{x-2} \cdot q^{x+2} & =(p q)^{2 x} \\ \left(\frac{p^x}{p^2}\right)\left(q^x\right)\left(q^2\right) & =(p q)^{2 x} \\ (p q)^x\left(\frac{q^2}{p^2}\right) & =(p q)^{2 x} \\ \left(\frac{q}{p}\right)^2 & =\frac{(p q)^{2 x}}{(p q)^x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^{2 x-x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^x(\text { Shown }) \end{aligned} $$
(b)
$$ \begin{aligned} \frac{k}{4-\sqrt{7}}+\sqrt{28} & =\frac{k}{4-\sqrt{7}}+\sqrt{28}\left(\frac{4-\sqrt{7}}{4-\sqrt{7}}\right) \\ & =\frac{k+\sqrt{28}(4-\sqrt{7})}{4-\sqrt{7}} \\ & =\frac{k+4 \sqrt{28}-\sqrt{196}}{4-\sqrt{7}} \\ & =\frac{k+4(2 \sqrt{7})-14}{4-\sqrt{7}} \\ & =\frac{k-14+8 \sqrt{7}}{4-\sqrt{7}} \times \frac{4+\sqrt{7}}{4+\sqrt{7}} \\ & =\frac{4 k-56+32 \sqrt{7}+k \sqrt{7}-14 \sqrt{7}+56}{16-7} \\ & =\frac{4 k+(18+k) \sqrt{7}}{9} \\ & =\frac{4 k}{9}+\left(\frac{18+k}{9}\right) \sqrt{7} \\ p=\frac{4 k}{9}, q= & \frac{18+k}{9} \end{aligned} $$
(a)
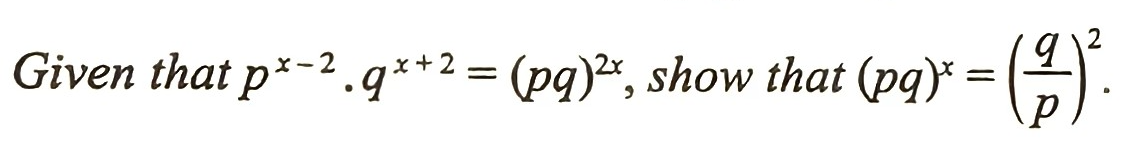
[3 marks]
(b)
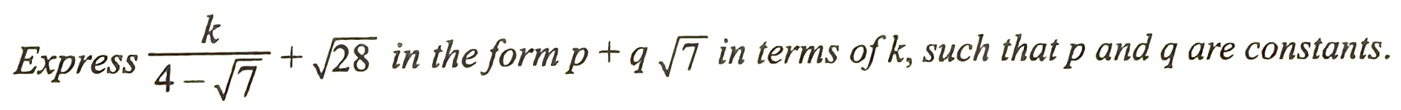
[3 marks]
Answer:
(a)
$$ \begin{aligned} p^{x-2} \cdot q^{x+2} & =(p q)^{2 x} \\ \left(\frac{p^x}{p^2}\right)\left(q^x\right)\left(q^2\right) & =(p q)^{2 x} \\ (p q)^x\left(\frac{q^2}{p^2}\right) & =(p q)^{2 x} \\ \left(\frac{q}{p}\right)^2 & =\frac{(p q)^{2 x}}{(p q)^x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^{2 x-x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^x(\text { Shown }) \end{aligned} $$
(b)
$$ \begin{aligned} \frac{k}{4-\sqrt{7}}+\sqrt{28} & =\frac{k}{4-\sqrt{7}}+\sqrt{28}\left(\frac{4-\sqrt{7}}{4-\sqrt{7}}\right) \\ & =\frac{k+\sqrt{28}(4-\sqrt{7})}{4-\sqrt{7}} \\ & =\frac{k+4 \sqrt{28}-\sqrt{196}}{4-\sqrt{7}} \\ & =\frac{k+4(2 \sqrt{7})-14}{4-\sqrt{7}} \\ & =\frac{k-14+8 \sqrt{7}}{4-\sqrt{7}} \times \frac{4+\sqrt{7}}{4+\sqrt{7}} \\ & =\frac{4 k-56+32 \sqrt{7}+k \sqrt{7}-14 \sqrt{7}+56}{16-7} \\ & =\frac{4 k+(18+k) \sqrt{7}}{9} \\ & =\frac{4 k}{9}+\left(\frac{18+k}{9}\right) \sqrt{7} \\ p=\frac{4 k}{9}, q= & \frac{18+k}{9} \end{aligned} $$