Question 1:
Diagram 1 shows sector BAC with centre A and sector COD with centre O. P lies on the straight line OD.
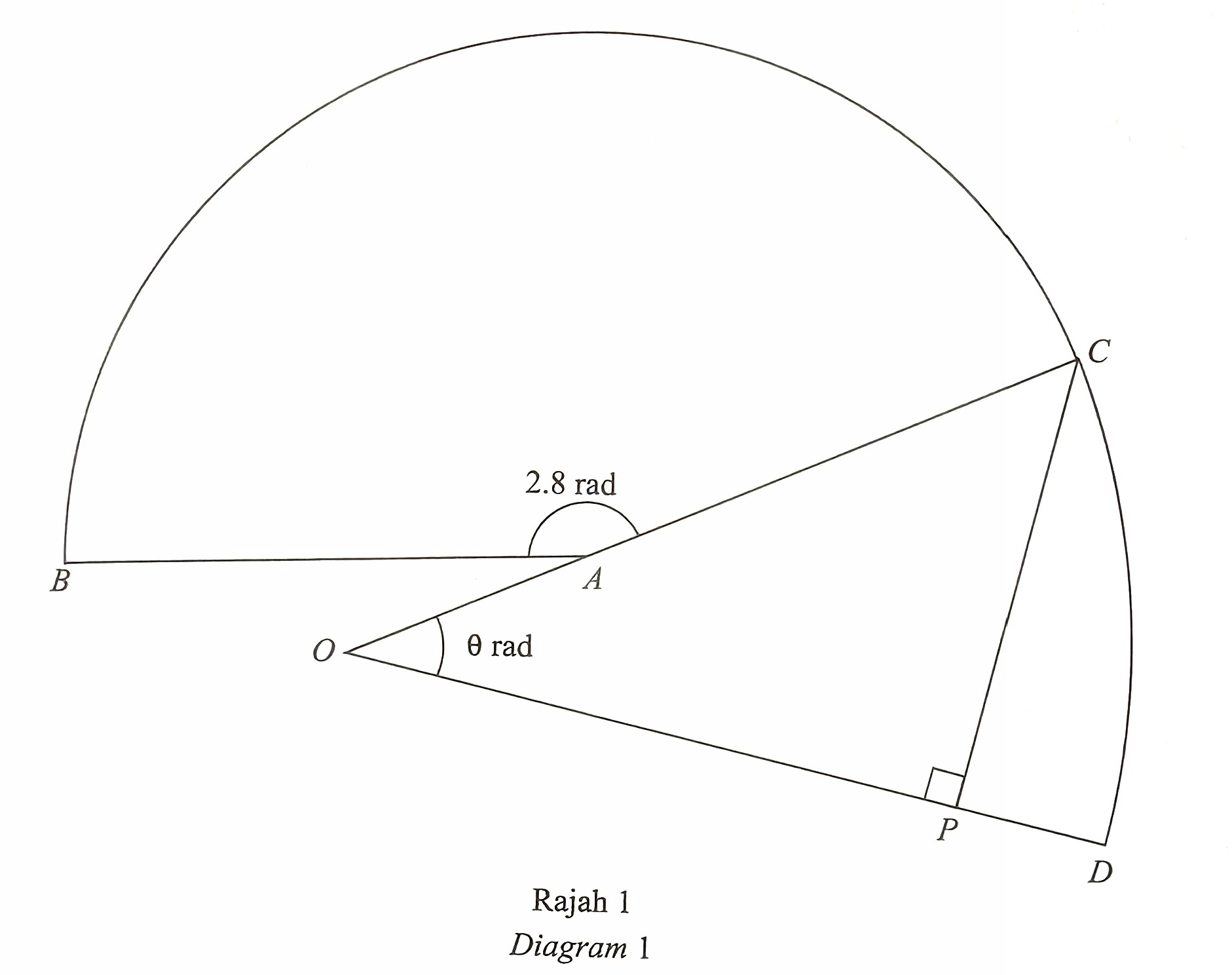
It is given that the area of sector BAC is 113.4 cm2, OA = ½ AC and CP = 7.74 cm.
[Use π = 3.142]
(a)(i) Find the length of AC, in cm.
(ii) Show that θ = 0.611 when rounded to three significant figures.
[4 marks]
(b) Hence, find the perimeter, in cm, of the whole diagram.
[3 marks]
Answer:
(a)(i)
$$ \begin{aligned} \text { Area } & = \frac{1}{2} r^2 \theta \\ \frac{1}{2}(A C)^2(2.8) & =113.4 \\ (A C)^2 & =\frac{113.4}{(2.8)\left(\frac{1}{2}\right)} \\ (A C)^2 & =81 \\ A C & =\sqrt{81} \\ A C & =9 \mathrm{~cm} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} O A & =\frac{1}{2} A C=4.5 \mathrm{~cm} \\ \therefore O C & =4.5 \mathrm{~cm}+9 \mathrm{~cm} \\ & =13.5 \mathrm{~cm} \\ \sin \theta & =\frac{C P}{O C} \\ \sin \theta & =\frac{7.74}{13.5} \\ \theta & =\sin ^{-1}\left(\frac{7.74}{13.5}\right) \\ \theta & =34.98^{\circ} \\ \theta & =0.6106 \mathrm{rad} \\ \theta & =0.611 \mathrm{rad} \end{aligned} $$
(b)
$$ \begin{aligned} S_{C D} & =(13.5)(0.611) \\ & =8.2485 \mathrm{~cm} \\ S_{B C} & =(9)(2.8) \\ & =25.2 \mathrm{~cm} \\ \text { Perimeter } & =A B+B C+C D+D O+O A \\ & =9+25.2+8.2485+13.5+4.5 \\ & =60.4485 \mathrm{~cm} \end{aligned} $$
Diagram 1 shows sector BAC with centre A and sector COD with centre O. P lies on the straight line OD.

It is given that the area of sector BAC is 113.4 cm2, OA = ½ AC and CP = 7.74 cm.
[Use π = 3.142]
(a)(i) Find the length of AC, in cm.
(ii) Show that θ = 0.611 when rounded to three significant figures.
[4 marks]
(b) Hence, find the perimeter, in cm, of the whole diagram.
[3 marks]
Answer:
(a)(i)
$$ \begin{aligned} \text { Area } & = \frac{1}{2} r^2 \theta \\ \frac{1}{2}(A C)^2(2.8) & =113.4 \\ (A C)^2 & =\frac{113.4}{(2.8)\left(\frac{1}{2}\right)} \\ (A C)^2 & =81 \\ A C & =\sqrt{81} \\ A C & =9 \mathrm{~cm} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} O A & =\frac{1}{2} A C=4.5 \mathrm{~cm} \\ \therefore O C & =4.5 \mathrm{~cm}+9 \mathrm{~cm} \\ & =13.5 \mathrm{~cm} \\ \sin \theta & =\frac{C P}{O C} \\ \sin \theta & =\frac{7.74}{13.5} \\ \theta & =\sin ^{-1}\left(\frac{7.74}{13.5}\right) \\ \theta & =34.98^{\circ} \\ \theta & =0.6106 \mathrm{rad} \\ \theta & =0.611 \mathrm{rad} \end{aligned} $$
(b)
$$ \begin{aligned} S_{C D} & =(13.5)(0.611) \\ & =8.2485 \mathrm{~cm} \\ S_{B C} & =(9)(2.8) \\ & =25.2 \mathrm{~cm} \\ \text { Perimeter } & =A B+B C+C D+D O+O A \\ & =9+25.2+8.2485+13.5+4.5 \\ & =60.4485 \mathrm{~cm} \end{aligned} $$