Question 6:
$$ \text { (a) Diagram } 5 \text { shows the graph of the function } f(x)=|x-3|+1 \text { for domain }-2 \leqslant x \leqslant 7 \text {. } $$
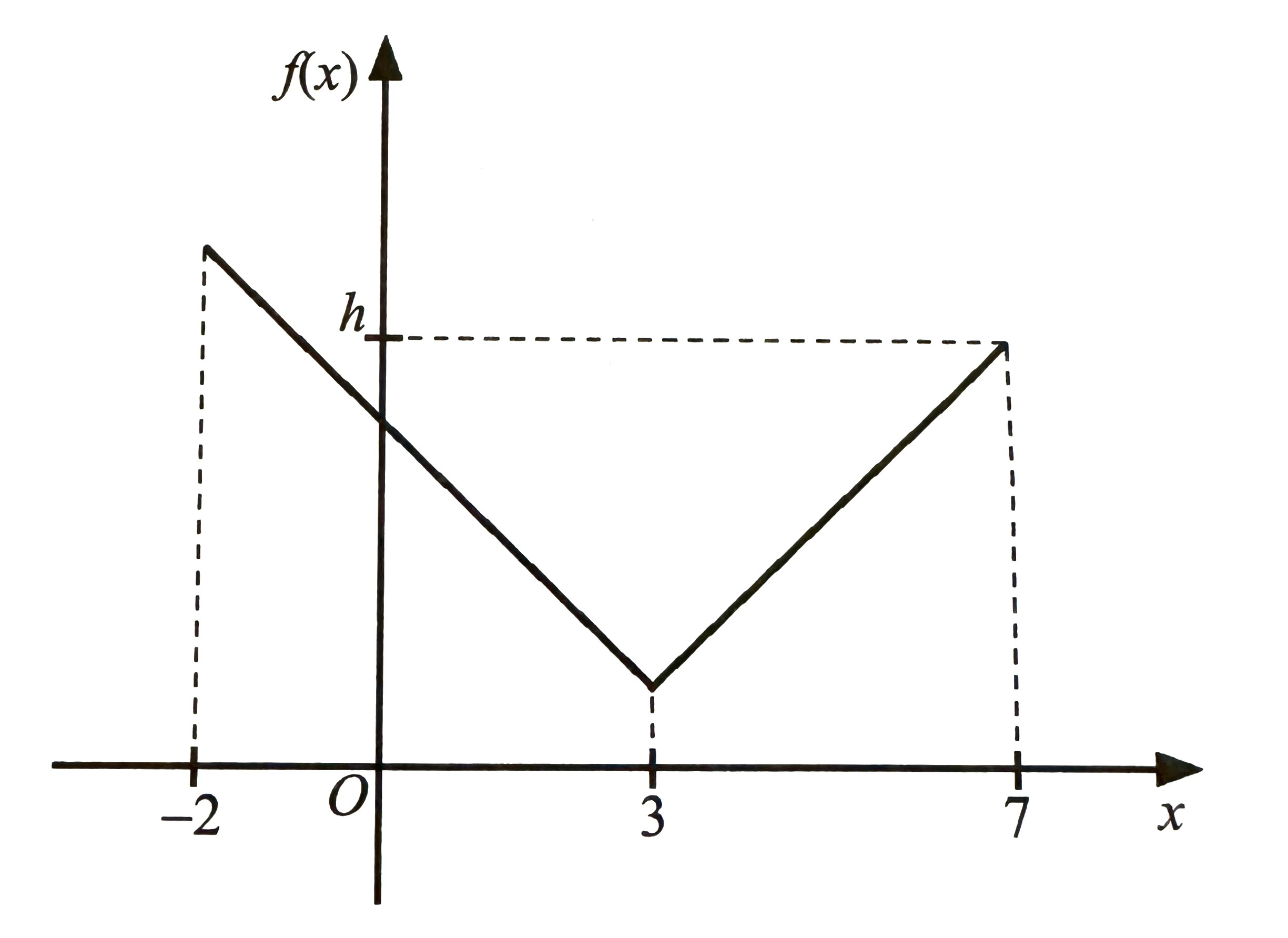
$$ \text { Find the value of the other object of } h \text {. [2 marks]} $$
$$ \text { (b) Given that the functions } f: x \rightarrow 4 x-1 \text { and } g: x \rightarrow 2 x+3 \text {, find } $$
$$ \text { (i) the value of } p \text { if f }{ }^{-1}(p)=2 \text {, } $$
$$ \text { (ii) the value of } x \text { if } f g(x)=5 f(2) \text {. [4 marks]} $$
Solution:
(a)
$$ \begin{aligned} f(7) & =h \\ |7-3|+1 & =h \\ |4|+1 & =h \\ h & =5 \end{aligned} $$
$$ \begin{aligned} f(x) & =5 \\ |x-3|+1 & =5 \\ |x-3| & =4 \end{aligned} $$
$$ \begin{aligned} x-3 & =4 \\ x & =7 \end{aligned} $$
$$ \begin{aligned} x-3 & =-4 \\ x & =-1 \end{aligned} $$
$$ \therefore \text { Object of } h \text { is }-1 \text {. } $$
(b)(i)
$$ \begin{aligned} &f(x)=4 x-1\\ &\begin{aligned} & \text { Let } 4 x-1=y \\ & 4 x=y+1 \\ & x=\frac{y+1}{4} \\ & f^1(x)=\frac{x+1}{4} \end{aligned} \end{aligned} $$
$$ \begin{aligned} f^1(p) & =2 \\ \frac{p+1}{4} & =2 \\ p+1 & =8 \\ p & =7 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} f g(x) & =5 f(2) \\ f(2 x+3) & =5[4(2)-1] \\ 4(2 x+3)-1 & =5(8-1) \\ 8 x+12-1 & =5(7) \\ 8 x+11 & =35 \\ 8 x & =24 \\ x & =3 \end{aligned} $$
$$ \text { (a) Diagram } 5 \text { shows the graph of the function } f(x)=|x-3|+1 \text { for domain }-2 \leqslant x \leqslant 7 \text {. } $$
$$ \text { Find the value of the other object of } h \text {. [2 marks]} $$
$$ \text { (b) Given that the functions } f: x \rightarrow 4 x-1 \text { and } g: x \rightarrow 2 x+3 \text {, find } $$
$$ \text { (i) the value of } p \text { if f }{ }^{-1}(p)=2 \text {, } $$
$$ \text { (ii) the value of } x \text { if } f g(x)=5 f(2) \text {. [4 marks]} $$
Solution:
(a)
$$ \begin{aligned} f(7) & =h \\ |7-3|+1 & =h \\ |4|+1 & =h \\ h & =5 \end{aligned} $$
$$ \begin{aligned} f(x) & =5 \\ |x-3|+1 & =5 \\ |x-3| & =4 \end{aligned} $$
$$ \begin{aligned} x-3 & =4 \\ x & =7 \end{aligned} $$
$$ \begin{aligned} x-3 & =-4 \\ x & =-1 \end{aligned} $$
$$ \therefore \text { Object of } h \text { is }-1 \text {. } $$
(b)(i)
$$ \begin{aligned} &f(x)=4 x-1\\ &\begin{aligned} & \text { Let } 4 x-1=y \\ & 4 x=y+1 \\ & x=\frac{y+1}{4} \\ & f^1(x)=\frac{x+1}{4} \end{aligned} \end{aligned} $$
$$ \begin{aligned} f^1(p) & =2 \\ \frac{p+1}{4} & =2 \\ p+1 & =8 \\ p & =7 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} f g(x) & =5 f(2) \\ f(2 x+3) & =5[4(2)-1] \\ 4(2 x+3)-1 & =5(8-1) \\ 8 x+12-1 & =5(7) \\ 8 x+11 & =35 \\ 8 x & =24 \\ x & =3 \end{aligned} $$
Question 7:
(a) Diagram 6 shows a curve and a tangent to the curve.
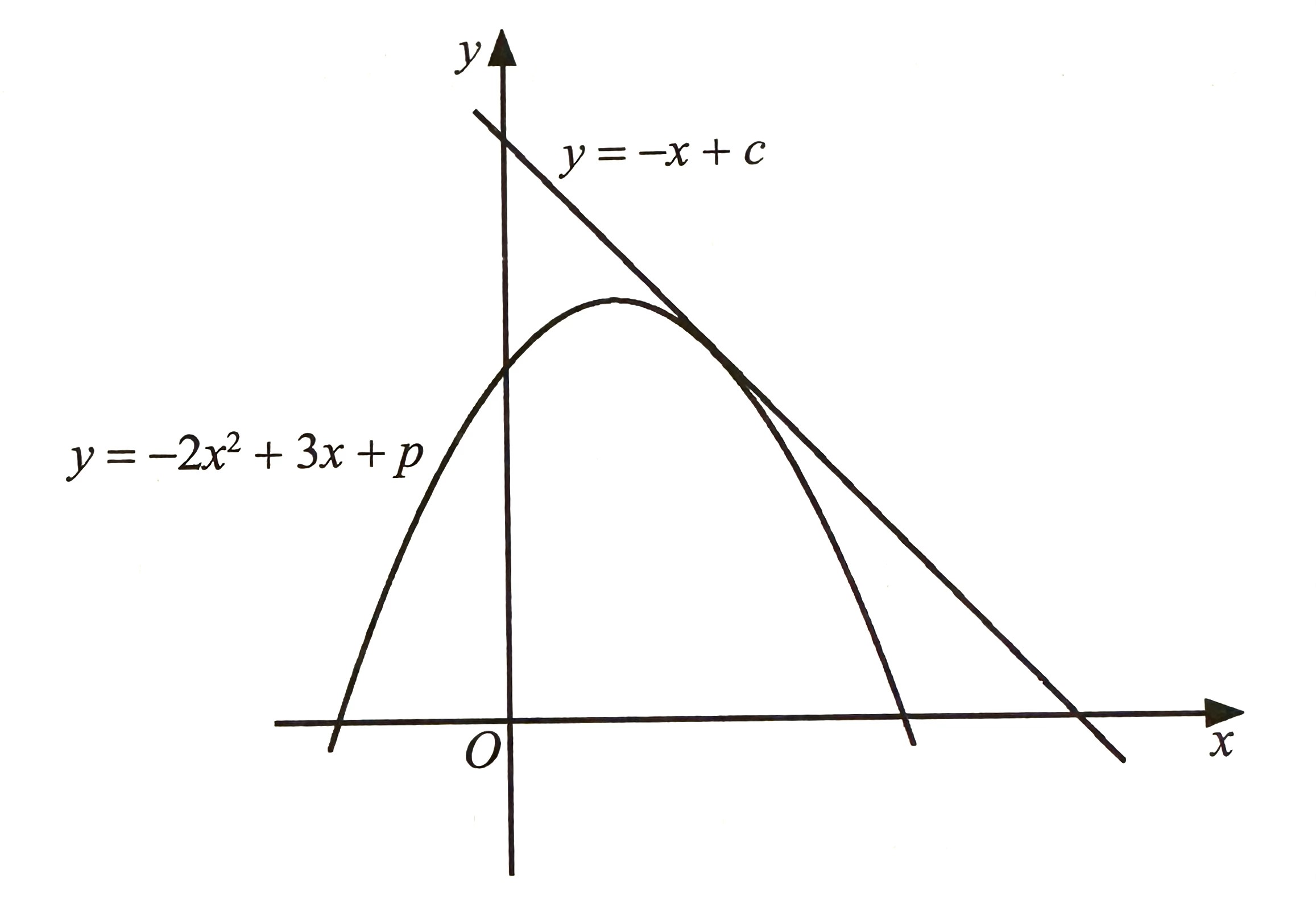Express p in terms of c.
[3 marks]
(b) Find the range of values of x for (x + 1)(-3x – 3) < (x – 1) by using the table method.
[2 marks]
(c) It is given that p and 2p are the roots of the quadratic equation 2x2 + 6x + 4p2 = 0.
Find the quadratic equation with roots (p – 1) and (p + 1).
[3 marks]
Solution:
(a)
$$ \begin{aligned} &\begin{aligned} & y=-x+c \ldots(1) \\ & y=-2 x^2+3 x+p \ldots(2) \end{aligned}\\ &\begin{aligned} (1)=(2):-2 x^2+3 x+p & =-x+c \\ -2 x^2+3 x+p+x-c & =0 \\ 2 x^2-4 x-p+c & =0 \\ a=2, \quad b=-4, \quad c & =-p+c \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Tangent to the curve, }\\ &\begin{aligned} b^2-4 a c & =0 \\ (-4)^2-4(2)(-p+c) & =0 \\ 16-8(-p+c) & =0 \\ 16+8 p-8 c & =0 \\ 8 p & =8 c-16 \\ p & =c-2 \end{aligned} \end{aligned} $$
(b)
(x + 1)(-3x – 3) < x – 1
-3x2 – 3x – 3x – 3 – x + 1 < 0
-3x2 – 7x -2 < 0
3x2 – 7x – 2 > 0
(3x + 1)(x + 2) > 0
When (3x + 1)(x + 2) = 0,
x = -1/3 or -2
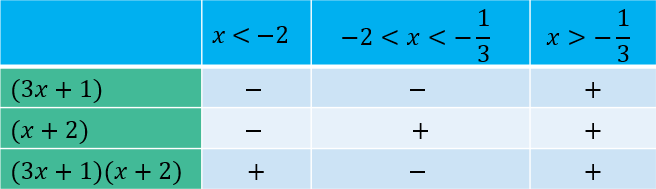
From the table,
(3x + 1)(x + 2) > 0 when x < -2 or x > -1/3
∴ x < -2 or x > -1/3
(c)
$$ \begin{aligned} & 2 x^2+6 x+4 p^2=0 \\ & \text { Roots }=p, 2 p \\ & \text { SOR: } p+2 p=-\frac{6}{2} \\ & 3 p=-3 \\ & p=-1 \end{aligned} $$
$$ \begin{aligned} &\text { New roots: }\\ &\begin{aligned} p-1 & =-1-1, \\ & =-2 \\ p+1 & =-1+1 \\ & =0 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { SOR: }-2+0=-2 \\ & \text { POR: }(-2)(0)=0 \end{aligned} $$
$$ \begin{aligned} & x^2-(\mathrm{SOR}) x+(\mathrm{POR})=0 \\ & x^2-(-2) x+0=0 \\ & x^2+4 x=0 \end{aligned} $$
(a) Diagram 6 shows a curve and a tangent to the curve.
Express p in terms of c. [3 marks]
(b) Find the range of values of x for (x + 1)(-3x – 3) < (x – 1) by using the table method.
[2 marks]
(c) It is given that p and 2p are the roots of the quadratic equation 2x2 + 6x + 4p2 = 0.
Find the quadratic equation with roots (p – 1) and (p + 1).
[3 marks]
Solution:
(a)
$$ \begin{aligned} &\begin{aligned} & y=-x+c \ldots(1) \\ & y=-2 x^2+3 x+p \ldots(2) \end{aligned}\\ &\begin{aligned} (1)=(2):-2 x^2+3 x+p & =-x+c \\ -2 x^2+3 x+p+x-c & =0 \\ 2 x^2-4 x-p+c & =0 \\ a=2, \quad b=-4, \quad c & =-p+c \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Tangent to the curve, }\\ &\begin{aligned} b^2-4 a c & =0 \\ (-4)^2-4(2)(-p+c) & =0 \\ 16-8(-p+c) & =0 \\ 16+8 p-8 c & =0 \\ 8 p & =8 c-16 \\ p & =c-2 \end{aligned} \end{aligned} $$
(b)
(x + 1)(-3x – 3) < x – 1
-3x2 – 3x – 3x – 3 – x + 1 < 0
-3x2 – 7x -2 < 0
3x2 – 7x – 2 > 0
(3x + 1)(x + 2) > 0
When (3x + 1)(x + 2) = 0,
x = -1/3 or -2
From the table,
(3x + 1)(x + 2) > 0 when x < -2 or x > -1/3
∴ x < -2 or x > -1/3
(c)
$$ \begin{aligned} & 2 x^2+6 x+4 p^2=0 \\ & \text { Roots }=p, 2 p \\ & \text { SOR: } p+2 p=-\frac{6}{2} \\ & 3 p=-3 \\ & p=-1 \end{aligned} $$
$$ \begin{aligned} &\text { New roots: }\\ &\begin{aligned} p-1 & =-1-1, \\ & =-2 \\ p+1 & =-1+1 \\ & =0 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { SOR: }-2+0=-2 \\ & \text { POR: }(-2)(0)=0 \end{aligned} $$
$$ \begin{aligned} & x^2-(\mathrm{SOR}) x+(\mathrm{POR})=0 \\ & x^2-(-2) x+0=0 \\ & x^2+4 x=0 \end{aligned} $$