Question 13 (10 marks):
Table 2 shows the information related to four ingredients, J, K, L and M, used in the production of a type of energy drinks.
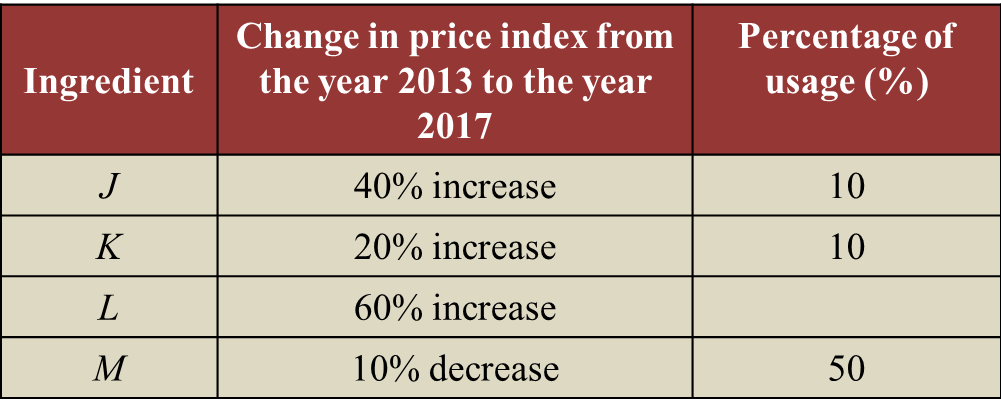
The production cost for this energy drinks is RM47600 in the year 2017.
(a) If the price of ingredient K in the year 2013 is RM4.20, find its price in the year 2017.
(b) Percentage of usage for several ingredients was given in Table 2.
Calculate the corresponding production cost in the year 2013.
(c) The production cost is expected to increase by 50% from the year 2017 to the year 2019.
Calculate the percentage of changes in production cost from the year 2013 to the year 2019.
Solution:
(a)
(b)
(c)
Table 2 shows the information related to four ingredients, J, K, L and M, used in the production of a type of energy drinks.

The production cost for this energy drinks is RM47600 in the year 2017.
(a) If the price of ingredient K in the year 2013 is RM4.20, find its price in the year 2017.
(b) Percentage of usage for several ingredients was given in Table 2.
Calculate the corresponding production cost in the year 2013.
(c) The production cost is expected to increase by 50% from the year 2017 to the year 2019.
Calculate the percentage of changes in production cost from the year 2013 to the year 2019.
Solution:
(a)
(b)
(c)
Question 14 (10 marks):
Solution by scale drawing is not accepted.
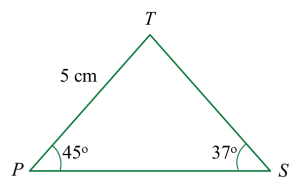
Diagram 8 shows a transparent prism with a rectangular base PQRS. The inclined surface PQUT is a square with sides 12 cm and the inclined surface RSTU is a rectangle. PTS is a uniform cross section of the prism. QST is a green coloured plane in the prism.
 It is given that ∠PST = 37o and ∠TPS = 45o.
It is given that ∠PST = 37o and ∠TPS = 45o.
Find
(a) the length, in cm, of ST,
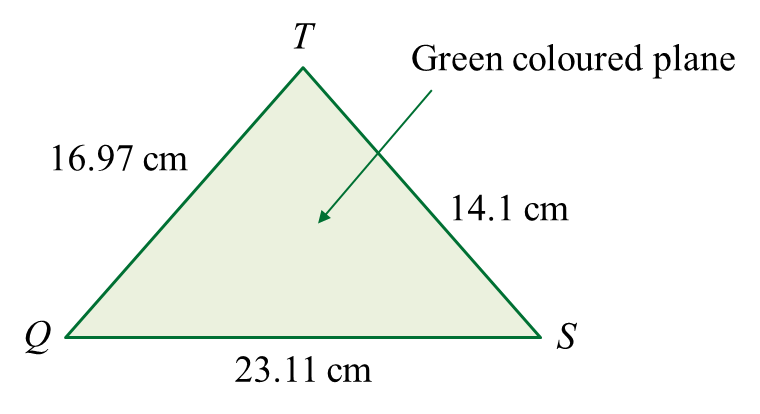
(b) the area, in cm2, of the green coloured plane.
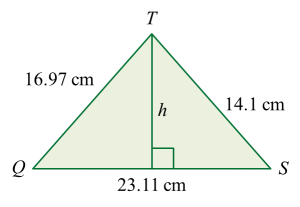
(c) the shortest length, in cm, from point T to the straight line QS.
Solution:
(a)
(b)
(c)
Solution by scale drawing is not accepted.
Diagram 8 shows a transparent prism with a rectangular base PQRS. The inclined surface PQUT is a square with sides 12 cm and the inclined surface RSTU is a rectangle. PTS is a uniform cross section of the prism. QST is a green coloured plane in the prism.
 It is given that ∠PST = 37o and ∠TPS = 45o.
It is given that ∠PST = 37o and ∠TPS = 45o.Find
(a) the length, in cm, of ST,
(b) the area, in cm2, of the green coloured plane.
(c) the shortest length, in cm, from point T to the straight line QS.
Solution:
(a)

(b)

(c)
