Question 9:
Given that the quadratic function f(x) = 2x2 – px + p has a minimum value of –18 at x = 1.
(a) Find the values of p and q.
(b) With the value of p and q found in (a), find the values of x, where graph f(x) cuts the x-axis.
(c) Hence, sketch the graph of f(x).
Solution:
(a)
(b)
(c)
Given that the quadratic function f(x) = 2x2 – px + p has a minimum value of –18 at x = 1.
(a) Find the values of p and q.
(b) With the value of p and q found in (a), find the values of x, where graph f(x) cuts the x-axis.
(c) Hence, sketch the graph of f(x).
Solution:
(a)
(b)
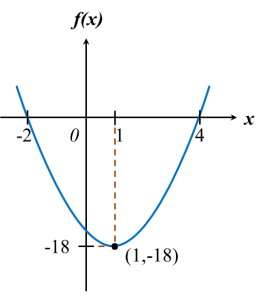
(c)

Question 10:
(a) Find the range of values of k if the equation x2 – kx + 3k – 5 = 0 does not have real roots.
(b) Show that the quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.
Solution:
(a)
Graph function y = (k – 2)(k – 10) cuts the horizontal line at k = 2 and k = 10 when b2 – 4ac < 0.

The range of values of k that satisfy the inequality above is 2 < k < 10.
(b)
The minimum value of (h + 1) + 8 is 8, a positive value. Therefore, b2 – 4ac > 0 for all values of h.
Hence, quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.
(a) Find the range of values of k if the equation x2 – kx + 3k – 5 = 0 does not have real roots.
(b) Show that the quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.
Solution:
(a)
Graph function y = (k – 2)(k – 10) cuts the horizontal line at k = 2 and k = 10 when b2 – 4ac < 0.

The range of values of k that satisfy the inequality above is 2 < k < 10.
(b)
The minimum value of (h + 1) + 8 is 8, a positive value. Therefore, b2 – 4ac > 0 for all values of h.
Hence, quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.