Question 26 (SPM 2018 – 3 marks):
Faizal has a rectangular plywood with a dimension 3x metre in length and 2x metre in width. He cuts part of the plywood into a square shape with sides of x metre to make a table surface.
Find the range of values of x if the remaining area of the plywood is at least (x2 + 4) metre2.
Solution:
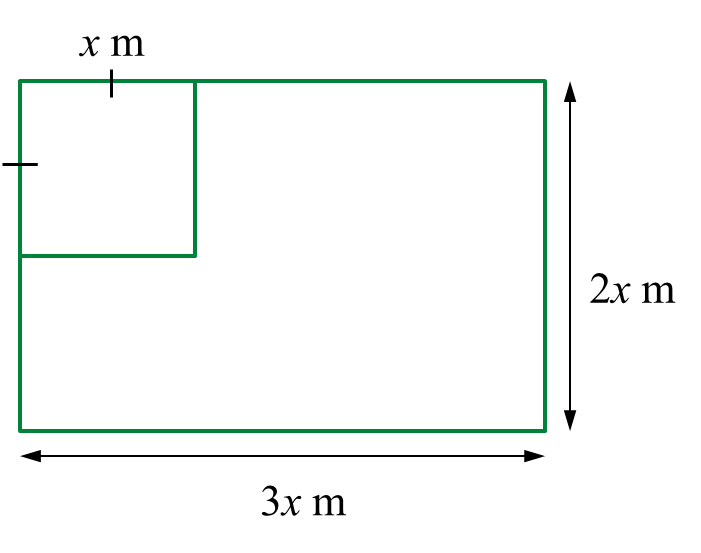
Area of plywood – area of square ≥ (x2 + 4)
3x(2x) – x2 ≥ x2 + 4
6x2 – x2 – x2 ≥ 4
4x2 ≥ 4
x2 – 1 ≥ 0
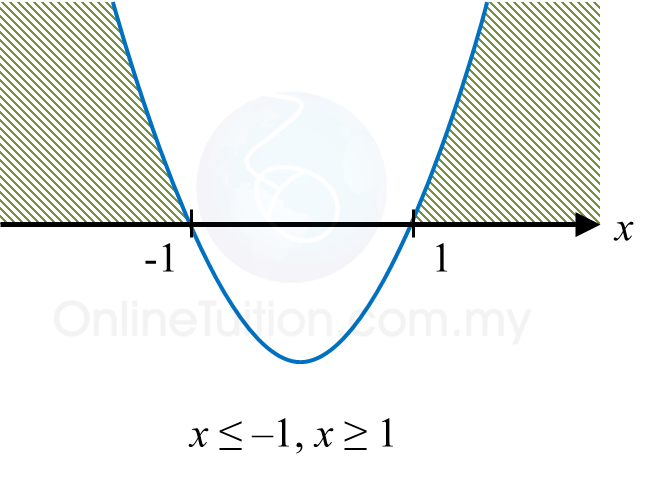
(x + 1)(x – 1) ≥ 0
x ≤ –1 or x ≥ 1
Thus, x ≥ 1 (length is > 0)
Faizal has a rectangular plywood with a dimension 3x metre in length and 2x metre in width. He cuts part of the plywood into a square shape with sides of x metre to make a table surface.
Find the range of values of x if the remaining area of the plywood is at least (x2 + 4) metre2.
Solution:

Area of plywood – area of square ≥ (x2 + 4)
3x(2x) – x2 ≥ x2 + 4
6x2 – x2 – x2 ≥ 4
4x2 ≥ 4
x2 – 1 ≥ 0
(x + 1)(x – 1) ≥ 0
x ≤ –1 or x ≥ 1
Thus, x ≥ 1 (length is > 0)

Question 27 (SPM 2018 – 3 marks):
It is given that the curve y = (p – 2)x2 – x + 7, where p is a constant, intersects with the straight line y = 3x + 5 at two points.
Find the range of values of p.
Solution:
It is given that the curve y = (p – 2)x2 – x + 7, where p is a constant, intersects with the straight line y = 3x + 5 at two points.
Find the range of values of p.
Solution:
Question 28 (SPM 2018 – 3 marks):
It is given that the quadratic equation hx2 – 3x + k = 0, where h and k are constants has roots β and 2β.
Express h in terms of k.
Solution:
It is given that the quadratic equation hx2 – 3x + k = 0, where h and k are constants has roots β and 2β.
Express h in terms of k.
Solution:
Question 29 (SPM 2015 – 3 marks):
The graph of a quadratic function f(x) =px2 – 8x + q, where p and q are constants, has a maximum point.
(a) Given p is an integer such that -2 < p < 2, state the value of p.
(b) Using the answer from 3(a), find the value of q when the graph touches the x-axis at one point.
[3 marks]
Answer:
(a) p = -1
(b)
$$ \begin{aligned} & f(x)=-x^2-8 x+q \\ & a=-1, b=-8, c=q \\ & b^2-4 a c=0 \\ & (-8)^2-4(-1) q=0 \\ & 64+4 q=0 \\ & 4 q=-64 \\ & q=-16 \end{aligned} $$
The graph of a quadratic function f(x) =px2 – 8x + q, where p and q are constants, has a maximum point.
(a) Given p is an integer such that -2 < p < 2, state the value of p.
(b) Using the answer from 3(a), find the value of q when the graph touches the x-axis at one point.
[3 marks]
Answer:
(a) p = -1
(b)
$$ \begin{aligned} & f(x)=-x^2-8 x+q \\ & a=-1, b=-8, c=q \\ & b^2-4 a c=0 \\ & (-8)^2-4(-1) q=0 \\ & 64+4 q=0 \\ & 4 q=-64 \\ & q=-16 \end{aligned} $$
Question 30 (SPM 2015 – 2 marks):
It is given -7 is one of the roots of the quadratic equation (x + k)2 = 16, where k is a constant.
Find the values of k.
[2 marks]
Answer:
$$ \begin{aligned} (x+k)^2= & 16 \\ \sqrt{(-7+k)^2} & = \pm \sqrt{16} \\ -7+k & = \pm 4 \\ -7+k & =4 \\ k & =4+7=11 \\ -7+k & =-4 \\ k & =-4+7=3 \end{aligned} $$
It is given -7 is one of the roots of the quadratic equation (x + k)2 = 16, where k is a constant.
Find the values of k.
[2 marks]
Answer:
$$ \begin{aligned} (x+k)^2= & 16 \\ \sqrt{(-7+k)^2} & = \pm \sqrt{16} \\ -7+k & = \pm 4 \\ -7+k & =4 \\ k & =4+7=11 \\ -7+k & =-4 \\ k & =-4+7=3 \end{aligned} $$
Good questions helps me to clear my problem