Question 1:
Solution:
(a)(b)
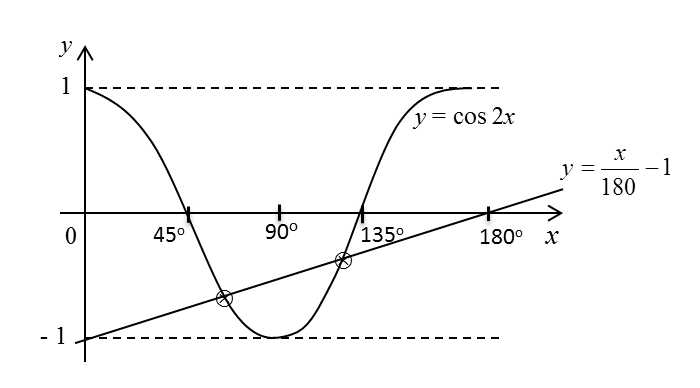
(a) Sketch the graph of y = cos 2x for 0° ≤ x ≤ 180°.
(b) Hence, by drawing a suitable straight line on the same axes, find the number of solutions satisfying the equation
for 0° ≤ x ≤ 180°.
Solution:
(a)(b)

Question 2:
Solution:
(a)
(b)(i)
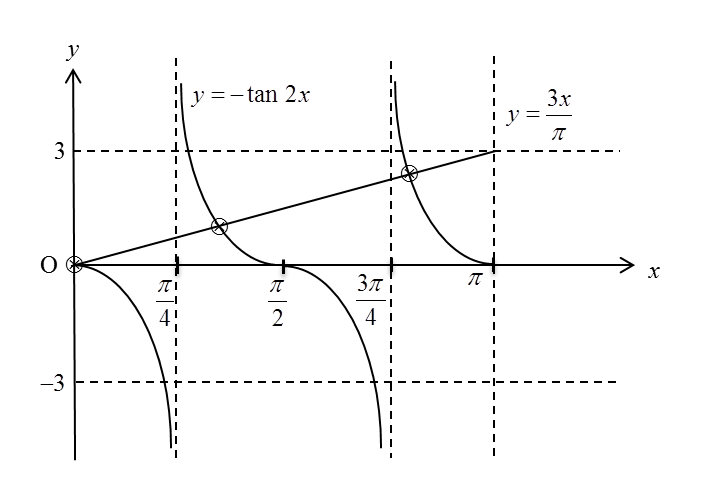
(b)(ii)
When x = 0, y = 0.
(a) Prove that
(b)(i) Sketch the graph of y = – tan 2x for 0 ≤ x ≤ π .
(b)(ii) Hence, by drawing a suitable straight line on the same axes, find the number of solutions satisfying the equation
for 0 ≤ x ≤ π .
State the number of solutions.
Solution:
(b)(i)
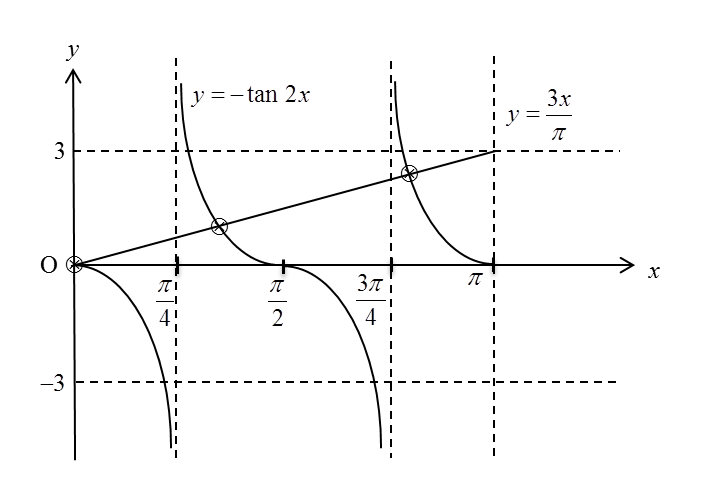
When x = 0, y = 0.
When x = π, y = 3.
Number of solutions = 3