Question 14:
Solution by graph sketching is not accepted.
Particle P moves along a straight line such that fixed points A and B lie on the straight line. Its velocity, in m s-1, is given by v = 3t2 + 4t – 15, such that t is the time, in seconds, after passing through point A towards point B.
[Assume motion to the right is positive]
(a) Determine whether point A is to the left or to the right of point B. Justify your answer.
[1 mark]
(b) Find the acceleration, in m s-2, of the particle at t = 1.3 s.
[2 marks]
(c) If the distance between points A and B is 15 m , determine whether the particle will pass point B or not. Give a reason for your answer.
[4 marks]
(d) Particle Q moves along the same straight line such that its velocity, v = m s-1, is given by v = 2t2 – 7t + 6, such that t is the time, in seconds, after passing point A.
Determine the range of time, in seconds, when both particles move to the left.
[3 marks]
Answer:
(a)
$$ \text { When } t=0, v=3(0)^2+4(0)-15 $$
$$ v=-15 \mathrm{~m} \mathrm{~s}^{-1} \text { (particle is moving to the left) } $$
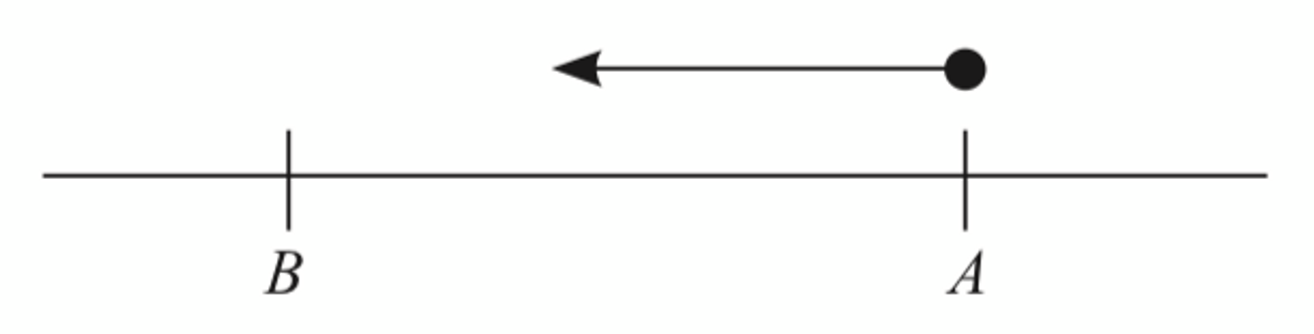
$$ \therefore \text { Point } A \text { is to the right of point } B \text {. } $$
(b)
$$ \begin{aligned} & a=\frac{\mathrm{d} v}{\mathrm{~d} t} \\ & a=6 t+4 ; \text { when } t=1.3 \mathrm{~s} \\ & a=6(1.3)+4 \\ & a=11.8 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Maximum, } s \text {; }\\ &\begin{aligned} & \begin{aligned} v=0 \Rightarrow & 3 t^2+4 t-15=0 \\ & (3 t-5)(t+3)=0 \\ 3 t-5= & 0, t+3=0 \\ t= & \frac{5}{3}, t=-3(\text { ignore }) \end{aligned} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & s=\int\left(3 t^2+4 t-15\right) \mathrm{d} t \\ & s=\frac{3 t^3}{3}+\frac{4 t^2}{2}-15 t+c \\ & s=t^3+2 t^2-15 t+c \end{aligned} $$
$$ \begin{aligned} & \text { when } t=0, s=0 \text {; } \\ & 0=(0)^3+2(0)^2-15(0)+c \\ & 0=c \\ & \therefore s=t^3+2 t^2-15 t \end{aligned} $$
$$ \begin{aligned} & \text { when } t=\frac{5}{3} \\ & s=\left(\frac{5}{3}\right)^3+2\left(\frac{5}{3}\right)^2-15\left(\frac{5}{3}\right) \\ & s=-14 \frac{22}{27} \mathrm{~m} \end{aligned} $$
Particle P will not pass through point B because it can only travel a maximum distance of 14 22/27 m from point A, whereas point B is 15 m away from A.
(d)
$$ \text { Particles move to the left, } v<0 $$
$$ \begin{aligned} v_P & <0 \\ 3 t^2+4 t-15 & <0 \\ (3 t-5)(t+3) & <0 \end{aligned} $$
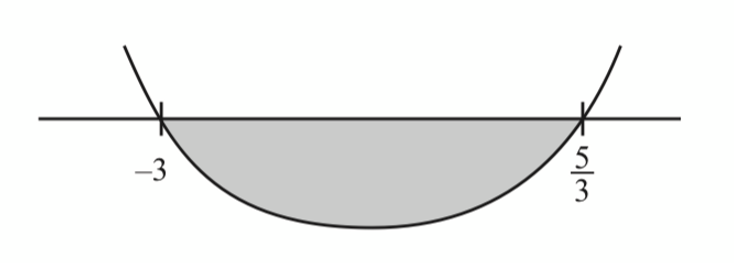 $$
3<t<\frac{5}{3}
$$
$$
3<t<\frac{5}{3}
$$
$$ \begin{aligned} v_Q & <0 \\ 2 t^2-7 t+6 & <0 \\ (2 t-3)(t-2) & <0 \end{aligned} $$
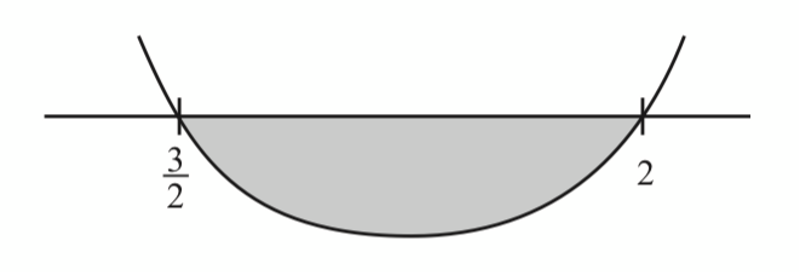 $$
\frac{3}{2}<t<2
$$
$$
\frac{3}{2}<t<2
$$
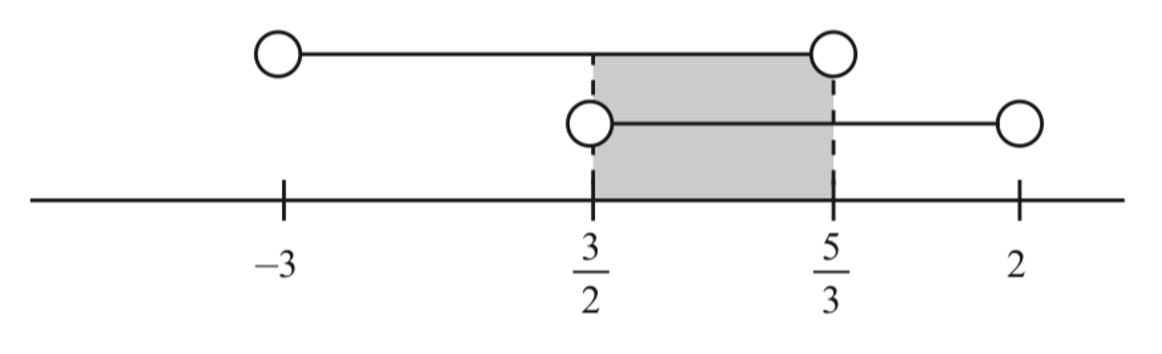
$$ \text { Both particles were move to the left when } \frac{3}{2}<t<\frac{5}{3} \text {. } $$
Solution by graph sketching is not accepted.
Particle P moves along a straight line such that fixed points A and B lie on the straight line. Its velocity, in m s-1, is given by v = 3t2 + 4t – 15, such that t is the time, in seconds, after passing through point A towards point B.
[Assume motion to the right is positive]
(a) Determine whether point A is to the left or to the right of point B. Justify your answer.
[1 mark]
(b) Find the acceleration, in m s-2, of the particle at t = 1.3 s.
[2 marks]
(c) If the distance between points A and B is 15 m , determine whether the particle will pass point B or not. Give a reason for your answer.
[4 marks]
(d) Particle Q moves along the same straight line such that its velocity, v = m s-1, is given by v = 2t2 – 7t + 6, such that t is the time, in seconds, after passing point A.
Determine the range of time, in seconds, when both particles move to the left.
[3 marks]
Answer:
(a)
$$ \text { When } t=0, v=3(0)^2+4(0)-15 $$
$$ v=-15 \mathrm{~m} \mathrm{~s}^{-1} \text { (particle is moving to the left) } $$

$$ \therefore \text { Point } A \text { is to the right of point } B \text {. } $$
(b)
$$ \begin{aligned} & a=\frac{\mathrm{d} v}{\mathrm{~d} t} \\ & a=6 t+4 ; \text { when } t=1.3 \mathrm{~s} \\ & a=6(1.3)+4 \\ & a=11.8 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Maximum, } s \text {; }\\ &\begin{aligned} & \begin{aligned} v=0 \Rightarrow & 3 t^2+4 t-15=0 \\ & (3 t-5)(t+3)=0 \\ 3 t-5= & 0, t+3=0 \\ t= & \frac{5}{3}, t=-3(\text { ignore }) \end{aligned} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & s=\int\left(3 t^2+4 t-15\right) \mathrm{d} t \\ & s=\frac{3 t^3}{3}+\frac{4 t^2}{2}-15 t+c \\ & s=t^3+2 t^2-15 t+c \end{aligned} $$
$$ \begin{aligned} & \text { when } t=0, s=0 \text {; } \\ & 0=(0)^3+2(0)^2-15(0)+c \\ & 0=c \\ & \therefore s=t^3+2 t^2-15 t \end{aligned} $$
$$ \begin{aligned} & \text { when } t=\frac{5}{3} \\ & s=\left(\frac{5}{3}\right)^3+2\left(\frac{5}{3}\right)^2-15\left(\frac{5}{3}\right) \\ & s=-14 \frac{22}{27} \mathrm{~m} \end{aligned} $$
Particle P will not pass through point B because it can only travel a maximum distance of 14 22/27 m from point A, whereas point B is 15 m away from A.
(d)
$$ \text { Particles move to the left, } v<0 $$
$$ \begin{aligned} v_P & <0 \\ 3 t^2+4 t-15 & <0 \\ (3 t-5)(t+3) & <0 \end{aligned} $$
 $$
3<t<\frac{5}{3}
$$
$$
3<t<\frac{5}{3}
$$$$ \begin{aligned} v_Q & <0 \\ 2 t^2-7 t+6 & <0 \\ (2 t-3)(t-2) & <0 \end{aligned} $$
 $$
\frac{3}{2}<t<2
$$
$$
\frac{3}{2}<t<2
$$
$$ \text { Both particles were move to the left when } \frac{3}{2}<t<\frac{5}{3} \text {. } $$