Question 13:
Mus wants to sell two types of crisps. Table 3 shows information relating to the two types of crisps.

(a) Mus has RM125 to buy the two types of crisps.
Write an inequality to represent this constraint.
[1 mark]
(b) The shaded region on the graph on page 150 represents the second constraint.
Write an inequality to represent the constraint.
[1 mark]
(c) The number of packets of crisp P sold is less than 3/2 of the number of packets of crisp Q sold.
On page 150, construct and label the region R which satisfies all the constraints and x > 0, y > 0.
[3 marks]
(d) Use the graph constructed in (c) to answer the following question:
(i) State the maximum number of packets of crisp P sold if 12 packets of crisp Q were sold.
(ii) Mus plans to save 50% of the total sales profit. He also needs to pay a wage of RM40 to a worker from the remainder. By drawing the objective function line to find the profit obtained, determine whether or not the selling prices are suitable. Give your justification.
[You may assume that he sells all of the crisps that he buys.]
[5 marks]

Answer:
(a)
$$ 4 x+2.5 y \leqslant 125 $$
(b)
$$ \begin{aligned} & y=\frac{20-0}{0-20} x+20 \\ & y=-x+20 \\ & y \geqslant 20-x \end{aligned} $$
(c)
$$ \begin{aligned} & x<\frac{3}{2} y \\ & y>\frac{2}{3} x \end{aligned} $$
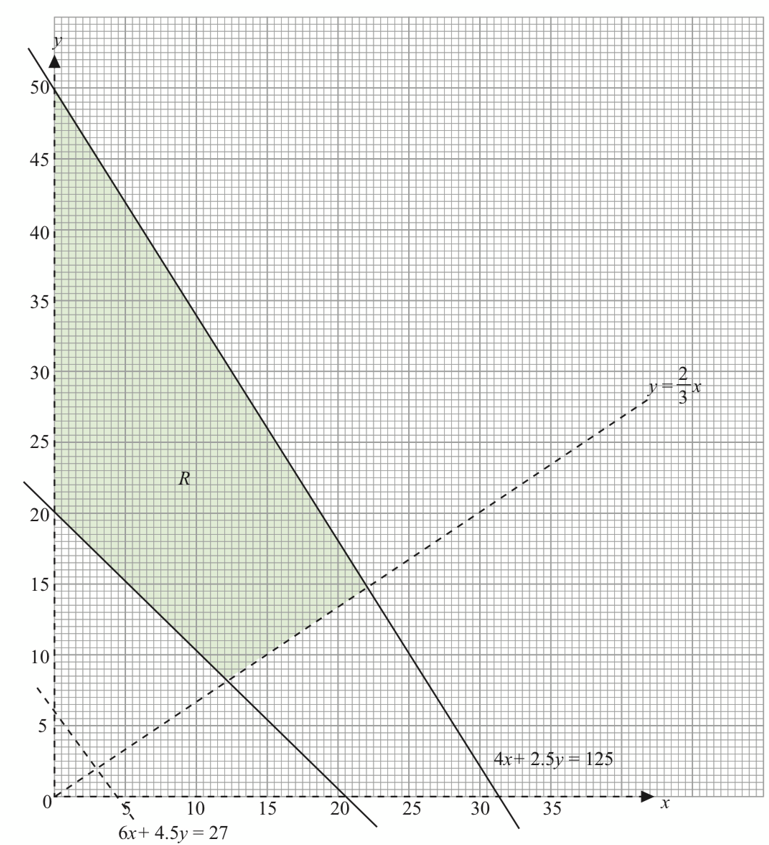
(d)(i) 17 packets
(d)(ii)
$$ \begin{aligned} \text { Profit, } P & =(10-4) x+(7-2.5) y \\ & =6 x+4.5 y \end{aligned} $$
$$ \text { Let } 6 x+4.5 y=27 $$
$$ \text { Optimal point: }(0,50) $$
$$ \begin{aligned} P & =6(0)+4.5(50) \\ & =\text { RM } 225 \end{aligned} $$
$$ \begin{aligned} \text { Saving } & =50 \% \times \text { RM225 } \\ & =\text { RM112.50 } \end{aligned} $$
$$ \begin{aligned} \text { Remaining } & =\text { RM112.50 }- \text { RM40 } \\ & =\text { RM72.50 } \end{aligned} $$
∴ Yes, the selling price is suitable because he is able to save money and for the wages and still have a balance of RM72.50 for his capital rolling.
Mus wants to sell two types of crisps. Table 3 shows information relating to the two types of crisps.

(a) Mus has RM125 to buy the two types of crisps.
Write an inequality to represent this constraint.
[1 mark]
(b) The shaded region on the graph on page 150 represents the second constraint.
Write an inequality to represent the constraint.
[1 mark]
(c) The number of packets of crisp P sold is less than 3/2 of the number of packets of crisp Q sold.
On page 150, construct and label the region R which satisfies all the constraints and x > 0, y > 0.
[3 marks]
(d) Use the graph constructed in (c) to answer the following question:
(i) State the maximum number of packets of crisp P sold if 12 packets of crisp Q were sold.
(ii) Mus plans to save 50% of the total sales profit. He also needs to pay a wage of RM40 to a worker from the remainder. By drawing the objective function line to find the profit obtained, determine whether or not the selling prices are suitable. Give your justification.
[You may assume that he sells all of the crisps that he buys.]
[5 marks]

Answer:
(a)
$$ 4 x+2.5 y \leqslant 125 $$
(b)
$$ \begin{aligned} & y=\frac{20-0}{0-20} x+20 \\ & y=-x+20 \\ & y \geqslant 20-x \end{aligned} $$
(c)
$$ \begin{aligned} & x<\frac{3}{2} y \\ & y>\frac{2}{3} x \end{aligned} $$

(d)(i) 17 packets
(d)(ii)
$$ \begin{aligned} \text { Profit, } P & =(10-4) x+(7-2.5) y \\ & =6 x+4.5 y \end{aligned} $$
$$ \text { Let } 6 x+4.5 y=27 $$
$$ \text { Optimal point: }(0,50) $$
$$ \begin{aligned} P & =6(0)+4.5(50) \\ & =\text { RM } 225 \end{aligned} $$
$$ \begin{aligned} \text { Saving } & =50 \% \times \text { RM225 } \\ & =\text { RM112.50 } \end{aligned} $$
$$ \begin{aligned} \text { Remaining } & =\text { RM112.50 }- \text { RM40 } \\ & =\text { RM72.50 } \end{aligned} $$
∴ Yes, the selling price is suitable because he is able to save money and for the wages and still have a balance of RM72.50 for his capital rolling.