Question 6:
Solution by scale drawing is not accepted.
Diagram 3 shows the positions of jetty O and kelongs K, L, R, S and T in the sea.
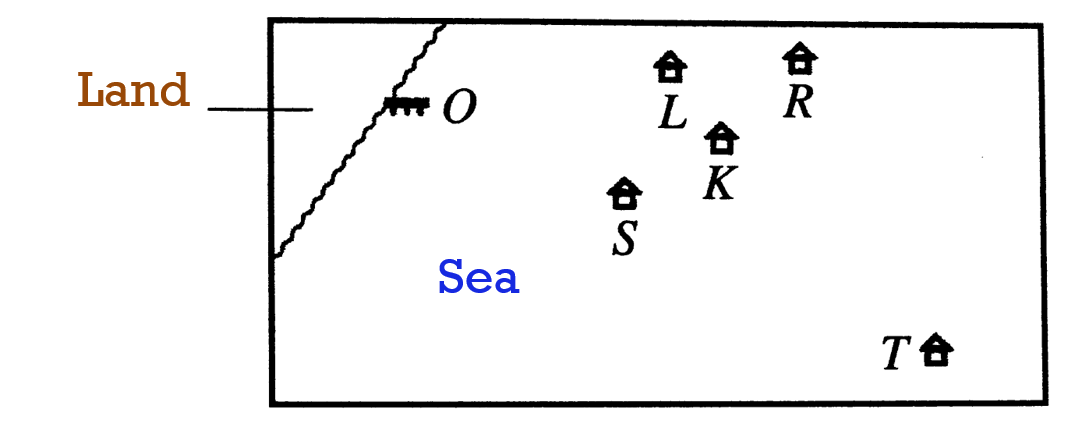Diagram 3
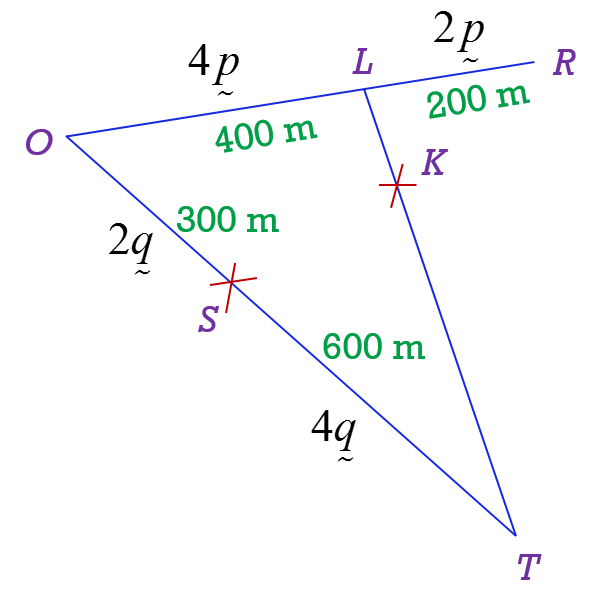
Kelong L is situated 400 m from jetty O and kelong R is situated 600 m from jetty O in the direction of OL. Kelong S is situated 300 m from jetty O and kelong T is situated 600 m from kelong 5 in the directions of OS. Kelongs L, K and T are situated on a straight line such that the distance of kelong K from kelong T is 5 times its distance from kelong L.
(a) By using to represent 100 m in the direction of OR and to represent 150 m in the direction of OT, express in terms of p˜ and q˜.
[3 marks]
(i) →OK, (ii) →RK.
(b) If Joe uses a binocular to observe kelong R from kelong S, determine whether kelong R can be seen without being blocked by kelong K or otherwise.
Prove you answer mathematically. [5 marks]
Solution:
(a)
KT=5KLKTKL=51KT:KL=5:1→OL=4p˜, →LR=2p˜, →OR=6p˜→OS=2q˜, →ST=4q˜, →OT=6q˜
(a)(i)
→OK=→OL+→LK =4p˜+16→LT =4p˜+16(−4p˜+6q˜) =4p˜−23p˜+q˜ =103p˜+q˜
(a)(ii)
→RK=→RO+→OK =−6p˜+103p˜+q˜ =−83p˜+q˜
(b)
→SR=→OR−→OS =6p˜−2q˜ =2(3p˜−q˜)→KR=−→RK =−(−83p˜+q˜) =83p˜−q˜→SR≠m→KR,m is a constant.
S, K and R are not collinear.
Hence, Kelong R can be seen without being blocked by Kelong K.
Solution by scale drawing is not accepted.
Diagram 3 shows the positions of jetty O and kelongs K, L, R, S and T in the sea.
Diagram 3Kelong L is situated 400 m from jetty O and kelong R is situated 600 m from jetty O in the direction of OL. Kelong S is situated 300 m from jetty O and kelong T is situated 600 m from kelong 5 in the directions of OS. Kelongs L, K and T are situated on a straight line such that the distance of kelong K from kelong T is 5 times its distance from kelong L.
(a) By using to represent 100 m in the direction of OR and to represent 150 m in the direction of OT, express in terms of p˜ and q˜.
[3 marks]
(i) →OK, (ii) →RK.
(b) If Joe uses a binocular to observe kelong R from kelong S, determine whether kelong R can be seen without being blocked by kelong K or otherwise.
Prove you answer mathematically. [5 marks]
Solution:
(a)
KT=5KLKTKL=51KT:KL=5:1→OL=4p˜, →LR=2p˜, →OR=6p˜→OS=2q˜, →ST=4q˜, →OT=6q˜
→OK=→OL+→LK =4p˜+16→LT =4p˜+16(−4p˜+6q˜) =4p˜−23p˜+q˜ =103p˜+q˜
(a)(ii)
→RK=→RO+→OK =−6p˜+103p˜+q˜ =−83p˜+q˜
(b)
→SR=→OR−→OS =6p˜−2q˜ =2(3p˜−q˜)→KR=−→RK =−(−83p˜+q˜) =83p˜−q˜→SR≠m→KR,m is a constant.
S, K and R are not collinear.
Hence, Kelong R can be seen without being blocked by Kelong K.