Question 8 (3 marks):
Diagram 3 shows vectors drawn on a square grid.
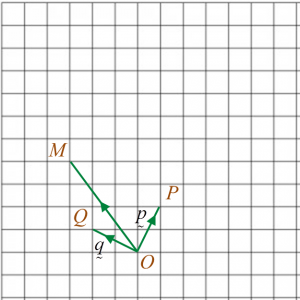 Diagram 3
Diagram 3
Solution:
(a)
(b)
Diagram 3 shows vectors drawn on a square grid.
 Diagram 3
Diagram 3Solution:
(a)
(b)
Question 9 (4 marks):
Solution:
(a)
(b)
Solution:
(a)
(b)
Question 10 (3 marks):
The following information refers to the equation of two straight lines, AB and CD.
Given the straight lines AB and CD are perpendicular to each other, express h in terms of k.
Solution:
The following information refers to the equation of two straight lines, AB and CD.
Given the straight lines AB and CD are perpendicular to each other, express h in terms of k.
Solution: