SPM Additional Mathematics 2017, Paper 1 (Question 4 – 7)

Question 4 (3 marks):
Diagram 4 shows a trapezium ABCD.

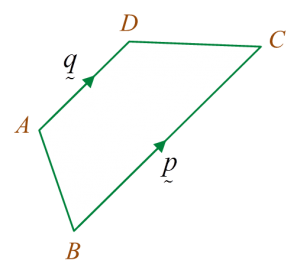Diagram 4

$\begin{array}{l}\text{Given }\underset{˜}{p}=\left(\begin{array}{l}3\\ 4\end{array}\right)\text{ and }\underset{˜}{q}=\left(\begin{array}{l}k-1\\ 2\end{array}\right)\text{, }\\ \text{where }k\text{ is a constant, find value of }k\text{.}\end{array}$


Solution:

$\begin{array}{l}\underset{˜}{p}=m\underset{˜}{q}\\ \left(\begin{array}{l}3\\ 4\end{array}\right)=m\left(\begin{array}{l}k-1\\ 2\end{array}\right)\\ \left(\begin{array}{l}3\\ 4\end{array}\right)=\left(\begin{array}{l}mk-m\\ 2m\end{array}\right)\\ \\ mk-m=3\mathrm{\dots \dots \dots .}\left(1\right)\\ 2m=4\mathrm{\dots \dots \dots \dots \dots .}\left(2\right)\\ \\ \text{From}\left(2\right):\\ 2m=4\\ m=2\\ \\ \text{Substitute }m=2\text{ into }\left(1\right):\\ 2k-2=3\\ 2k=3+2\\ 2k=5\\ k=\frac{5}{2}\end{array}$

Question 5 (3 marks):
$\text{Given }\frac{{25}^{h+3}}{{125}^{p-1}}\text{=1, express }p\text{ in terms of }h\text{.}$

Solution:
$\begin{array}{l}\frac{{25}^{h+3}}{{125}^{p-1}}=1\\ {25}^{h+3}={125}^{p-1}\\ {\left(5^2\right)}^{h+3}={\left(5^3\right)}^{p-1}\\ 5^{2h+6}=5^{3p-3}\\ 2h+6=3p-3\\ 3p=2h+9\\ p=\frac{2h+9}{3}\end{array}$

Question 6 (3 marks):
$\begin{array}{l}\text{Solve the equation:}\\ {\log }_{m}324-{\log }_{\sqrt{m}}2m=2\end{array}$

Solution:
$\begin{array}{l}{\log }_{m}324-{\log }_{\sqrt{m}}2m=2\\ {\log }_{m}324-\frac{{\log }_{m}2m}{{\log }_m{m}^{\frac{1}{2}}}=2\\ {\log }_{m}324-2\left(\frac{{\log }_{m}2m}{{\log }_{m}m}\right)=2\\ {\log }_{m}324-2{\log }_{m}2m=2\\ {\log }_{m}324-{\log }_m{\left(2m\right)}^2=lo{g}_m{m}^2\\ {\log }_m\left(\frac{324}{4m^2}\right)=lo{g}_m{m}^2\\ \frac{324}{4m^2}=m^2\\ 4m^4=324\\ m^4=81\\ m=\pm 3\left(-3\text{ is rejected}\right)\end{array}$

Question 7 (2 marks):
It is given that the n^th term of a geometric progression is $T_n=\frac{3r^{n-1}}{2},r\ne k.$  
State
(a) the value of k,
(b) the first term of progression.

Solution:
(a)
k = 0, k = 1 or k = -1 (Any one of these answer).

(b)
$\begin{array}{l}{T}_n=\frac{3}{2}{r}^{n-1}\\ T_1=\frac{3}{2}{r}^{1-1}\\ =\frac{3}{2}{r}^0\\ =\frac{3}{2}\left(1\right)\\ =\frac{3}{2}\end{array}$