Question 17 (3 marks):
It is given that , where c, n and p are constants.
Find the value of n and of p.
Solution:
It is given that , where c, n and p are constants.
Find the value of n and of p.
Solution:
Question 18 (3 marks):
A straight line passes through P(3, 1) and Q(12, 7). The point R divides the line segment PQ such that 2PQ = 3RQ.
Find the coordinates of R.
Solution:
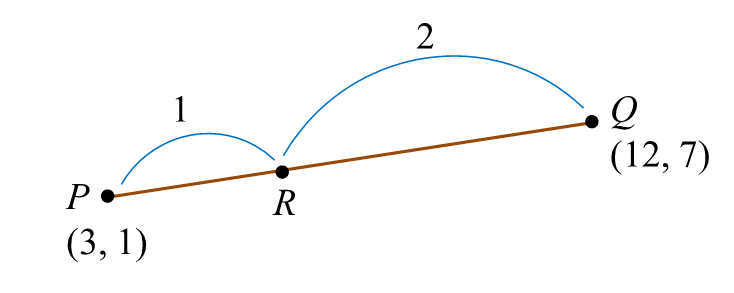
A straight line passes through P(3, 1) and Q(12, 7). The point R divides the line segment PQ such that 2PQ = 3RQ.
Find the coordinates of R.
Solution:

Question 19 (3 marks):
The variables x and y are related by the equation , where r is a constant. Diagram 8 shows a straight line graph obtained by plotting
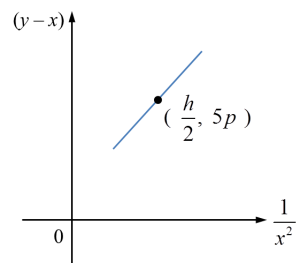 Diagram 8
Diagram 8
Express h in terms of p and r.
Solution:
The variables x and y are related by the equation , where r is a constant. Diagram 8 shows a straight line graph obtained by plotting
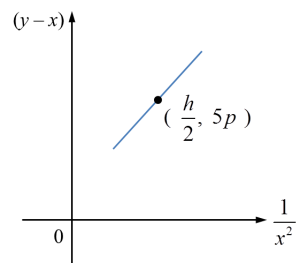 Diagram 8
Diagram 8Express h in terms of p and r.
Solution: