Question 15 (4 marks):
It is given that cos α = t where t is a constant and 0o ≤ α ≤ 90o.
Express in terms of t
(a) sin (180o + α),
(b) sec 2α.
Solution:
(a)
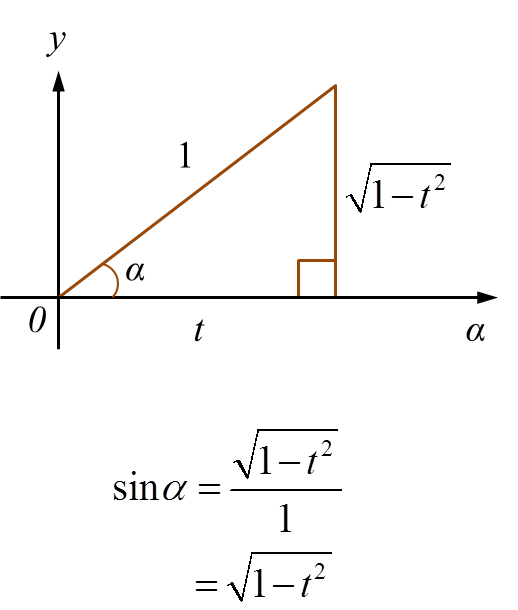
(b)
It is given that cos α = t where t is a constant and 0o ≤ α ≤ 90o.
Express in terms of t
(a) sin (180o + α),
(b) sec 2α.
Solution:
(a)
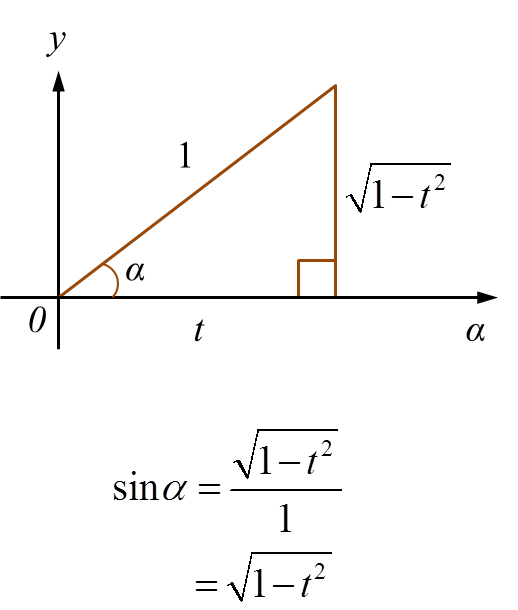
(b)
Question 16 (3 marks):
Diagram 7 shows two sectors AOD and BOC of two concentric circles with centre O.
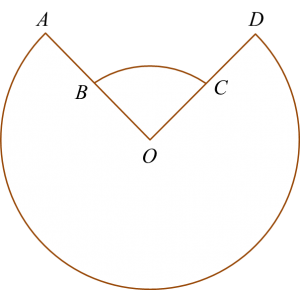 Diagram 7
Diagram 7
The angle subtended at the centre O by the major arc AD is 7α radians and the perimeter of the whole diagram is 50 cm.
Given OB = r cm, OA = 2OB and ∠BOC = 2α, express r in terms of α.
Solution:
Diagram 7 shows two sectors AOD and BOC of two concentric circles with centre O.
 Diagram 7
Diagram 7The angle subtended at the centre O by the major arc AD is 7α radians and the perimeter of the whole diagram is 50 cm.
Given OB = r cm, OA = 2OB and ∠BOC = 2α, express r in terms of α.
Solution: