3.8.5 Integration, Long Questions (Question 9)

Question 9:

Diagram 4 shows part of a curve x = y² + 2. The gradient of a straight line QR is –1.

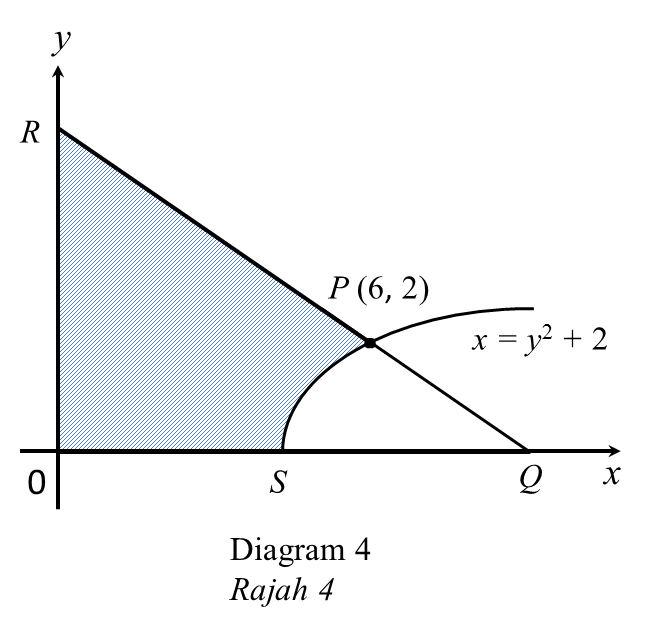Find

(a) the equation of PQ, [2 marks]

(b) the area of shaded region, [4 marks]

Solution:

(a)

y – 2 = –1 (x – 6)

y = –x + 6 + 2

y = –x + 8

(b)

y = –x + 8, at y-axis, x = 0

y = 8

Point R = (0, 8)

Area of shaded region

= Area under the curve + Area of triangle

\begin{array}{l} = \int_{0}^{2} x d y + \frac{1}{2} (8 - 2) (6) \\ = \int_{0}^{2} (y^{2} + 2) d y + \frac{1}{2} (6) (6) \\ = {[\frac{y^{3}}{3} + 2 y]}_{0}^{2} + 18 \\ = [\frac{2^{3}}{3} + 2 (2) - 0] + 18 \\ = \frac{20}{3} + 18 \\ = 24 \frac{2}{3} u n i t^{2} \end{array}

(c)

Volume of revolution

= Volume under the curve + Volume of cone

\begin{array}{l} = π \int_{0}^{2} x^{2} d y + \frac{1}{3} π r^{2} h \\ = π \int_{0}^{2} {(y^{2} + 2)}^{2} d y + \frac{1}{3} π {(6)}^{2} (6) \\ = π \int_{0}^{2} (y^{4} + 4 y^{2} + 4) d y + 72 π \\ = π {[\frac{y^{5}}{5} + \frac{4 y^{3}}{3} + 4 y]}_{0}^{2} + 72 π \\ = π [\frac{2^{5}}{5} + \frac{4 {(2)}^{3}}{3} + 4 (2) - 0] + 72 π \\ = π [\frac{32}{5} + \frac{32}{3} + 8] + 72 π \\ = \frac{376}{15} π + 72 π \\ = 97 \frac{1}{15} π {unit}^{3} \end{array}