2.6 Gradients of Tangents, Equations of Tangents and Normals

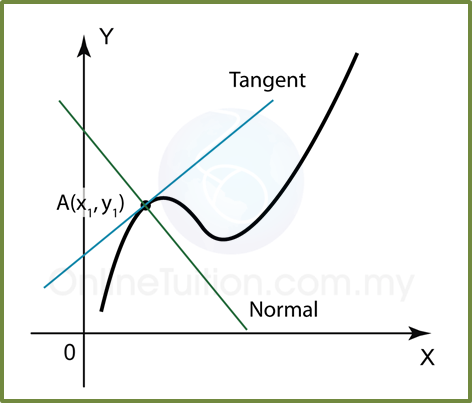
2.6 Gradients of Tangents, Equations of Tangents and Normals

If A(x₁, y₁) is a point on a line y = f(x), the gradient of the line (for a straight line) or the gradient of the tangent of the line (for a curve) is the value of

$\frac{d y}{d x}$ when x = x₁.

(A) Gradient of tangent at A(x₁, y₁):

(B) Equation of tangent:

(C) Gradient of normal at A(x₁, y₁):

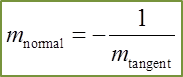
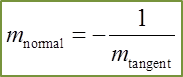
(D) Equation of normal :

Example 1 (Find the Equation of Tangent)

Given that

$y = \frac{4}{{(3 x - 1)}^{2}}$ . Find the equation of the tangent at the point (1, 1).

Solution:

$\begin{array}{l} y = \frac{4}{{(3 x - 1)}^{2}} = 4 {(3 x - 1)}^{- 2} \\ \frac{d y}{d x} = - 2.4 {(3 x - 1)}^{- 3} .3 \\ \frac{d y}{d x} = \frac{- 24}{{(3 x - 1)}^{3}} \\ At point (1, 1), \frac{d y}{d x} = \frac{- 24}{{[3 (1) - 1]}^{3}} = \frac{- 24}{8} = - 3 \\ Equation of tangent at point (1, 1) is, \\ y - 1 = - 3 (x - 1) \\ y - 1 = - 3 x + 3 \\ y = - 3 x + 4 \end{array}$

Example 2 (Find the Equation of Normal)

Find the gradient of the curve

$y = \frac{7}{3 x + 4}$ at the point (-1, 7). Hence, find the equation of the normal to the curve at this point.

Solution:

$\begin{array}{l} y = \frac{7}{3 x + 4} = 7 {(3 x + 4)}^{- 1} \\ \frac{d y}{d x} = - 7 {(3 x + 4)}^{- 2} .3 \\ \frac{d y}{d x} = \frac{- 21}{{(3 x + 4)}^{2}} \\ At point (- 1, 7), \frac{d y}{d x} = \frac{- 21}{{[3 (- 1) + 4]}^{2}} = - 21 \\ Gradient of the normal = \frac{1}{21} \\ Equation of the normal is \\ y - y_{1} = m (x - x_{1}) \\ y - 7 = \frac{1}{21} (x - (- 1)) \\ 21 y - 147 = x + 1 \\ 21 y - x - 148 = 0 \end{array}$

Leave a Comment Cancel reply