8.7.4 Vectors, SPM Practice (Question 7 & 8)

Question 7:
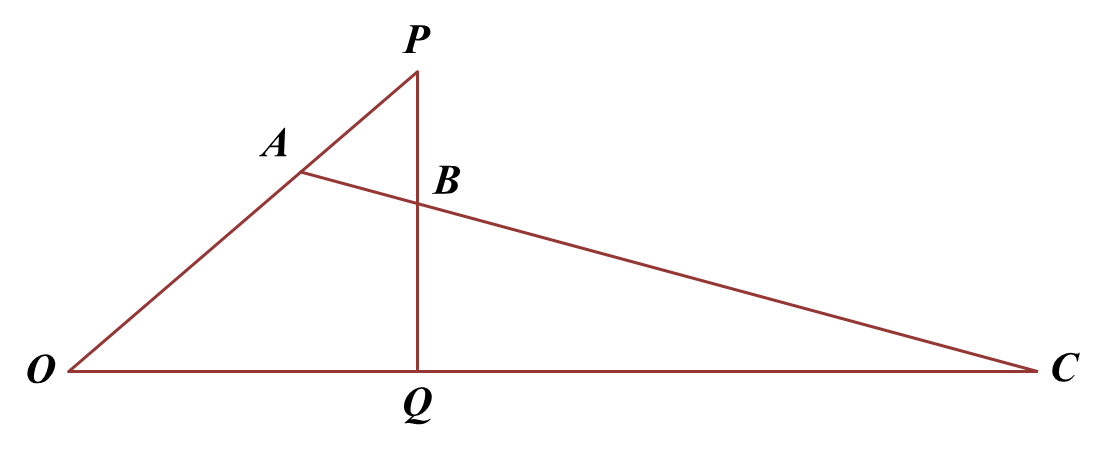
Diagram below shows quadrilateral OPBC. The straight line AC intersects the straight line PQ at point B.

$\begin{array}{l}\text{It is given that }\overrightarrow{OP}=\underset{˜}{a},\overrightarrow{OQ}=\underset{˜}{b},\overrightarrow{OA}=4\overrightarrow{AP},\overrightarrow{OC}=3\overrightarrow{OQ},\overrightarrow{PB}=h\overrightarrow{PQ}\text{ and}\\ \overrightarrow{AB}=k\overrightarrow{AC}.\\ \text{(a) Express }\overrightarrow{OB}\text{ in terms of }h\text{, }\underset{˜}{a}\text{ and }\underset{˜}{b}.\\ \text{(b) Express }\overrightarrow{OB}\text{ in terms of }k\text{, }\underset{˜}{a}\text{ and }\underset{˜}{b}.\\ \\ \text{(c)(i) Find the value of }h\text{ and of }k.\\ \text{(ii) Hence, state }\overrightarrow{OB}\text{ in terms of }\underset{˜}{a}\text{ and }\underset{˜}{b}.\end{array}$


Solution:
(a)
$\begin{array}{l}\overrightarrow{OB}=\overrightarrow{OP}+\overrightarrow{PB}\\ =\underset{˜}{a}+h\overrightarrow{PQ}\\ =\underset{˜}{a}+h\left(\overrightarrow{PO}+\overrightarrow{OQ}\right)\\ =\underset{˜}{a}+h\left(-\underset{˜}{a}+\underset{˜}{b}\right)\\ =\underset{˜}{a}-h\underset{˜}{a}+h\underset{˜}{b}\\ \overrightarrow{OB}=\left(1-h\right)\underset{˜}{a}+h\underset{˜}{b}\end{array}$


(b)
$\begin{array}{l}\overrightarrow{OB}=\overrightarrow{OP}+\overrightarrow{PB}\\ =\underset{˜}{a}+\overrightarrow{PA}+\overrightarrow{AB}\\ =\underset{˜}{a}+\left(-\frac{1}{5}\overrightarrow{OP}\right)+k\overrightarrow{AC}\\ =\underset{˜}{a}+\left(-\frac{1}{5}\underset{˜}{a}\right)+k\left(\overrightarrow{AO}+\overrightarrow{OC}\right)\\ =\frac{4}{5}\underset{˜}{a}+k\left(-\frac{4}{5}\overrightarrow{OP}+3\overrightarrow{OQ}\right)\\ =\frac{4}{5}\underset{˜}{a}+k\left(-\frac{4}{5}\underset{˜}{a}+3\underset{˜}{b}\right)\\ =\frac{4}{5}\underset{˜}{a}-\frac{4}{5}k\underset{˜}{a}+3k\underset{˜}{b}\\ \overrightarrow{OB}=\frac{4}{5}\left(1-k\right)\underset{˜}{a}+3k\underset{˜}{b}\end{array}$


(c)(i)
$\begin{array}{l}\left(1-h\right)\underset{˜}{a}+h\underset{˜}{b}=\frac{4}{5}\left(1-k\right)\underset{˜}{a}+3k\underset{˜}{b}\\ 1-h=\frac{4}{5}-\frac{4}{5}k\mathrm{\dots \dots \dots .}\left(1\right)\\ h=3k\mathrm{\dots \dots \dots .}\left(2\right)\\ \text{Substitute }\left(2\right)\text{ into the }\left(1\right)\\ 1-3k=\frac{4}{5}-\frac{4}{5}k\\ 5-15k=4-4k\\ 11k=1\\ k=\frac{1}{11}\\ \\ \text{Substitute }k=\frac{1}{11}\text{ into }\left(2\right)\\ h=3\left(\frac{1}{11}\right)\\ =\frac{3}{11}\end{array}$


(c)(ii)
$\begin{array}{l}\overrightarrow{OB}=\left(1-h\right)\underset{˜}{a}+h\underset{˜}{b}\\ \text{when }h=\frac{3}{11}\\ =\left(1-\frac{3}{11}\right)\underset{˜}{a}+\left(\frac{3}{11}\right)\underset{˜}{b}\\ =\frac{8}{11}\underset{˜}{a}+\frac{3}{11}\underset{˜}{b}\end{array}$

Question 8:
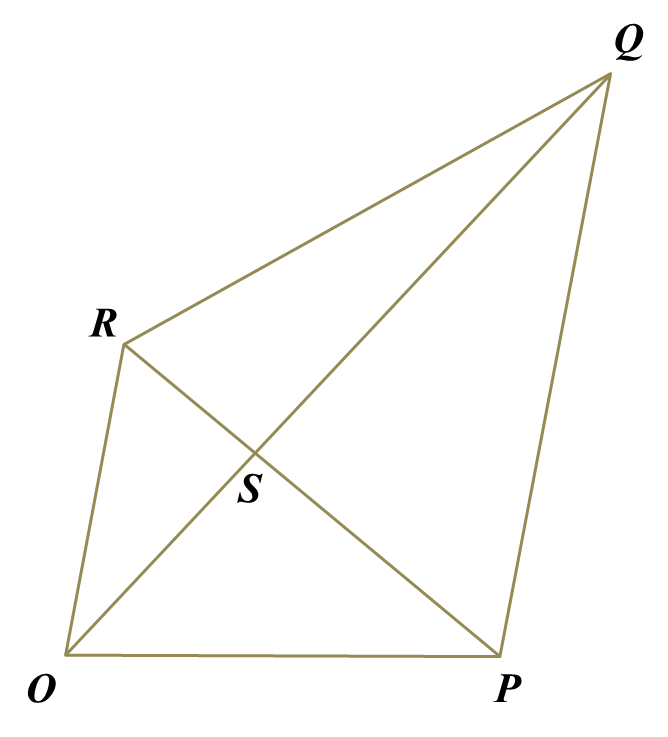
Diagram below shows quadrilateral OPQR. The straight line PR intersects the straight line OQ at point S.

$\begin{array}{l}\text{It is given that }\overrightarrow{OP}=7\underset{˜}{x},\overrightarrow{OR}=5\underset{˜}{y},PS:SR=3:1\text{ and }\overrightarrow{OR}\text{ is parallel to }\overrightarrow{PQ}.\\ \text{(a) Express in terms of }\underset{˜}{x}\text{ and }\underset{˜}{y},\\ \text{(i) }\overrightarrow{PR}\\ \text{(ii) }\overrightarrow{OS}\\ \\ \text{(b) Using }\overrightarrow{PQ}=m\overrightarrow{OR}\text{ and }\overrightarrow{SQ}=n\overrightarrow{OS},\text{ where }m\text{ and }n\text{ are constants,}\\ \text{ Find the value of }m\text{ and of }n.\\ \\ \text{(c) Given that }\left|\underset{˜}{y}\right|=4\text{ units and the area of }ORS{\text{ is 50 cm}}^2\text{, find the}\\ \text{ perpendicular distance from point }S\text{ to }OR\text{.}\end{array}$


Solution:
(a)(i)
$\begin{array}{l}\overrightarrow{PR}=\overrightarrow{PO}+\overrightarrow{OR}\\ =-7\underset{˜}{x}+5\underset{˜}{y}\end{array}$


(a)(ii)
$\begin{array}{l}\overrightarrow{OS}=\overrightarrow{OP}+\overrightarrow{PS}\\ =7\underset{˜}{x}+\frac{3}{4}\overrightarrow{PR}\\ =7\underset{˜}{x}+\frac{3}{4}\left(-7\underset{˜}{x}+5\underset{˜}{y}\right)\\ =7\underset{˜}{x}-\frac{21}{4}\underset{˜}{x}+\frac{15}{4}\underset{˜}{y}\\ =\frac{7}{4}\underset{˜}{x}+\frac{15}{4}\underset{˜}{y}\end{array}$


(b)
$\begin{array}{l}\overrightarrow{PS}=\overrightarrow{PQ}-\overrightarrow{SQ}\\ \frac{3}{4}\overrightarrow{PR}=m\overrightarrow{OR}-n\overrightarrow{OS}\\ \frac{3}{4}\left(-7\underset{˜}{x}+5\underset{˜}{y}\right)=m\left(5\underset{˜}{y}\right)-n\left(\frac{7}{4}\underset{˜}{x}+\frac{15}{4}\underset{˜}{y}\right)\\ -\frac{21}{4}\underset{˜}{x}+\frac{15}{4}\underset{˜}{y}=5m\underset{˜}{y}-\frac{7}{4}n\underset{˜}{x}-\frac{15}{4}n\underset{˜}{y}\\ -\frac{21}{4}\underset{˜}{x}+\frac{15}{4}\underset{˜}{y}=-\frac{7}{4}n\underset{˜}{x}+5m\underset{˜}{y}-\frac{15}{4}n\underset{˜}{y}\\ -\frac{7}{4}n=-\frac{21}{4}\\ 7n=21\\ n=3\\ \\ 5m-\frac{15}{4}n=\frac{15}{4}\\ 5m-\frac{15}{4}\left(3\right)=\frac{15}{4}\\ 5m-\frac{45}{4}=\frac{15}{4}\\ 5m=15\\ m=3\end{array}$


(c)
$\begin{array}{l}\text{Area of }\Delta ORS=50\\ \frac{1}{2}\times \left(5\underset{˜}{y}\right)\times t=50\\ \frac{1}{2}\times 5\left(4\right)\times t=50\\ 10t=50\\ t=5\\ \therefore \text{ Perpendicular distance from point }S\text{ to }OR=5\text{ units}\text{.}\end{array}$