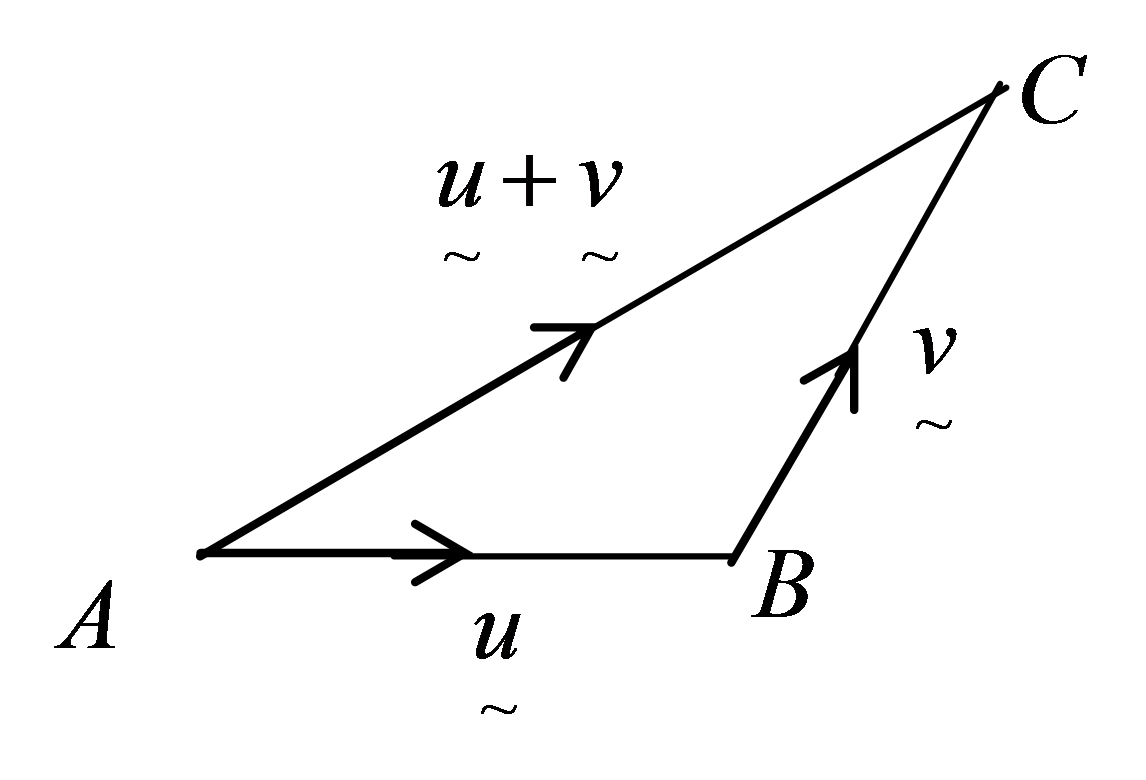8.3.1 Addition of Vectors - SPM Additional Mathematics

8.3 Addition and Subtraction of Vectors

8.3.1 Addition of Vectors

1. The addition of two vectors,

\underset{˜}{u} and \underset{˜}{v}

, can be written as

\underset{˜}{u} + \underset{˜}{v}

. The result of this addition is a vector which is called the resultant vector.

2. When two vectors with the same direction is added up, the resultant vector has

(a) the same direction with both the vectors.

(b) a magnitude equal to the sum of the magnitudes of both the vectors.

Addition of Non-parallel Vectors

1. Addition of two non-parallel vectors,

\underset{˜}{u} and \underset{˜}{v}

, can be shown by using two laws.

(a) Triangle Law of Addition

The resultant vector

\underset{˜}{u} + \underset{˜}{v}

is represented by the third side AC.

(b) Parallelogram Law of Addition

The resultant vector

\underset{˜}{u} + \underset{˜}{v}

is represented by the third side AC.

Example 1:

Find

(a) The resultant vector of the addition of the two parallel vectors above

(b) The magnitude of the resultant vector.

Solution:

(a)

Resultant vector

= addition of the two vectors

= \vec{P Q} + \vec{R S}

(b)

Magnitude of the resultant vector

\begin{array}{l} = | \vec{P Q} | + | \vec{R S} | \\ = | \sqrt{6^{2} + 8^{2}} | + | \sqrt{6^{2} + 8^{2}} | \\ = 10 + 10 \\ = 20 units \end{array}

Example 2:

The diagram above shows a parallelogram OABC. M is the midpoint of BC. Vector

\vec{O A} = \underset{˜}{a} and \vec{O C} = \underset{˜}{c} .

Find the following vectors in terms of

\underset{˜}{a} and \underset{˜}{c} .

\begin{array}{l} (a) \vec{O B} \\ (b) \vec{M B} \\ (c) \vec{O M} \end{array}

Solution:

(a)

\begin{array}{l} \vec{O B} = \vec{O A} + \vec{A B} \leftarrow Triangle Law of addition \\ = \vec{O A} + \vec{O C} \leftarrow \vec{A B} = \vec{O C} \\ = \underset{˜}{a} + \underset{˜}{c} \end{array}

(b)

\begin{array}{l} \vec{M B} = \frac{1}{2} \vec{C B} \leftarrow M is the midpoint of C B \\ = \frac{1}{2} \vec{O A} \\ = \frac{1}{2} \underset{˜}{a} \end{array}

(c)

\begin{array}{l} \vec{O M} = \vec{O C} + \vec{C M} \leftarrow Triangle Law of addition \\ = \vec{O C} + \vec{M B} \leftarrow \vec{C M} = \vec{M B} \\ = \underset{˜}{c} + \frac{1}{2} \underset{˜}{a} \end{array}

Leave a Comment Cancel reply