8.3.2 Subtraction of Vectors - SPM Additional Mathematics

8.3.2 Subtraction of Vectors

The subtraction of the vector

\underset{˜}{b}

from the vector

\underset{˜}{a}

is written as

\underset{˜}{a} - \underset{˜}{b}

. This operation can be considered as the addition of the vector

\underset{˜}{a}

with the negative vector of

\underset{˜}{b}

. Therefore

\underset{˜}{a} - \underset{˜}{b} = \underset{˜}{a} + (- \underset{˜}{b}) .

Example 1:

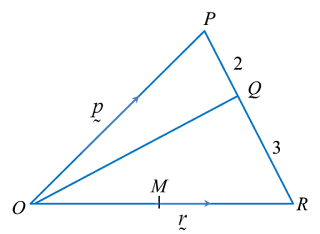
In the diagram above, vector

\vec{O P} = \underset{˜}{p}, \vec{O R} = \underset{˜}{r}

and Q divides PR in the ratio of 2 : 3. Find the following vectors in terms of

\underset{˜}{p} and \underset{˜}{r}

\begin{array}{l} (a) \vec{P R} \\ (b) \vec{O Q} \\ (c) \vec{Q M} if M is the midpoint of O R . \end{array}

Solution:

(a)

\begin{array}{l} \vec{P R} = \vec{P O} + \vec{O R} \\ = - \vec{O P} + \vec{O R} \\ = - \underset{˜}{p} + \underset{˜}{r} \end{array}

(b)

\begin{array}{l} \vec{O Q} = \vec{O P} + \vec{P Q} \\ = \vec{O P} + \frac{2}{5} \vec{P R} \\ = \underset{˜}{p} + \frac{2}{5} (- \underset{˜}{p} + \underset{˜}{r}) \\ = \underset{˜}{p} - \frac{2}{5} \underset{˜}{p} + \frac{2}{5} \underset{˜}{r} \\ = \frac{3}{5} \underset{˜}{p} + \frac{2}{5} \underset{˜}{r} \end{array}

(c)

\begin{array}{l} \vec{Q M} = \vec{Q O} + \vec{O M} \\ = - \vec{O Q} + \vec{O M} \\ = - \vec{O Q} + \frac{1}{2} \vec{O R} \\ = - (\frac{3}{5} \underset{˜}{p} + \frac{2}{5} \underset{˜}{r}) + \frac{1}{2} \underset{˜}{r} \\ = - \frac{3}{5} \underset{˜}{p} - \frac{2}{5} \underset{˜}{r} + \frac{1}{2} \underset{˜}{r} \\ = - \frac{3}{5} \underset{˜}{p} + \frac{1}{10} \underset{˜}{r} \end{array}