5.4.3 Sum of the First n Terms of Geometric Progressions
(F) Sum of the First n Terms of Geometric Progressions
(F) Sum of the First n Terms of Geometric Progressions
a = first term
r = common ratio
n = number of term
Sn = sum of the first n terms
Example 1:
Find the sum of each of the following geometric progressions.
(a) 1, 2, 4, … up to the first 7 terms
(b) 9, 3, 1, ⅓, … up to the first 6 terms
(c) 12, 3, …., [Smart TIPS: You can find n if you know the last term]
(c) 12, 3, …., [Smart TIPS: You can find n if you know the last term]
Solution:

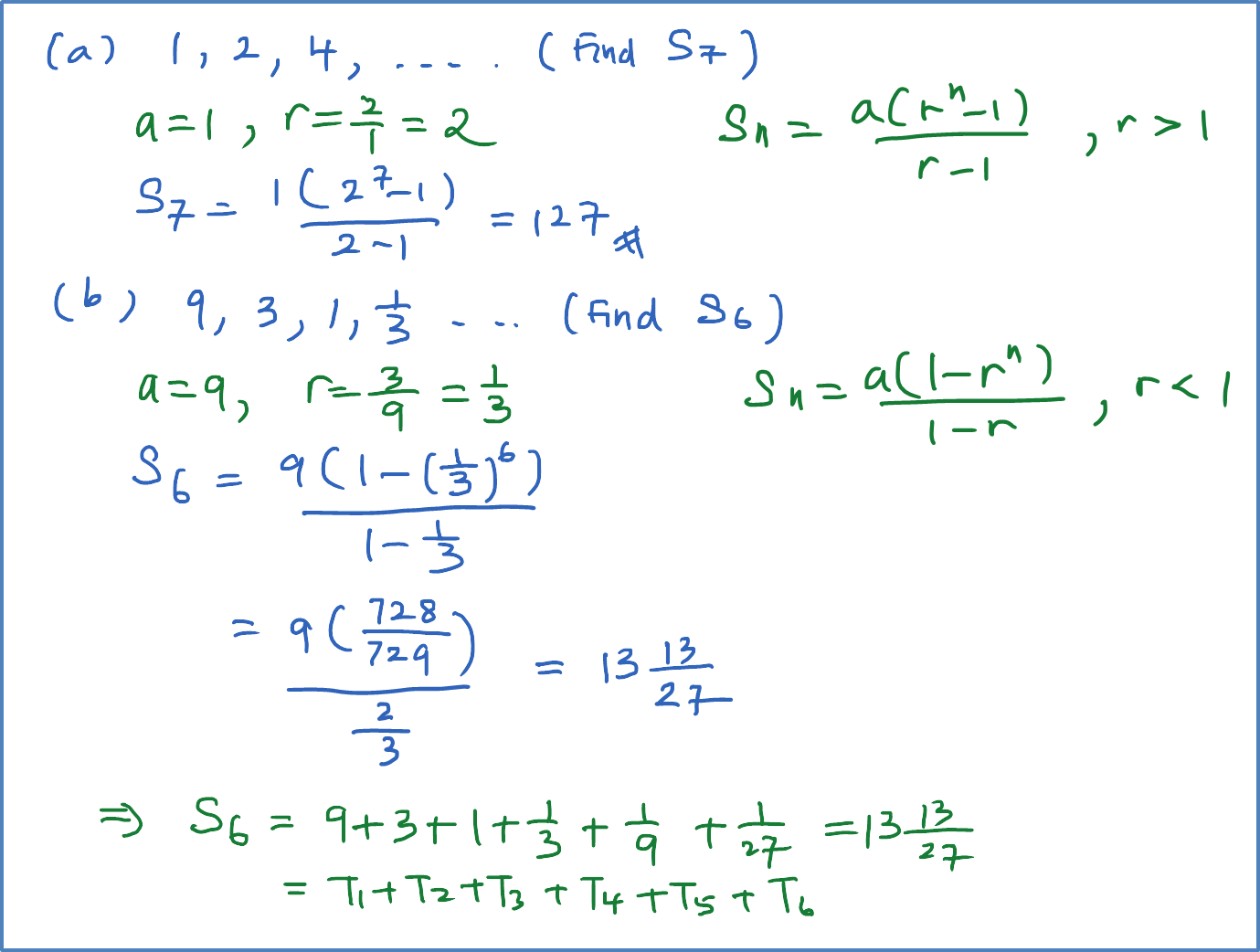


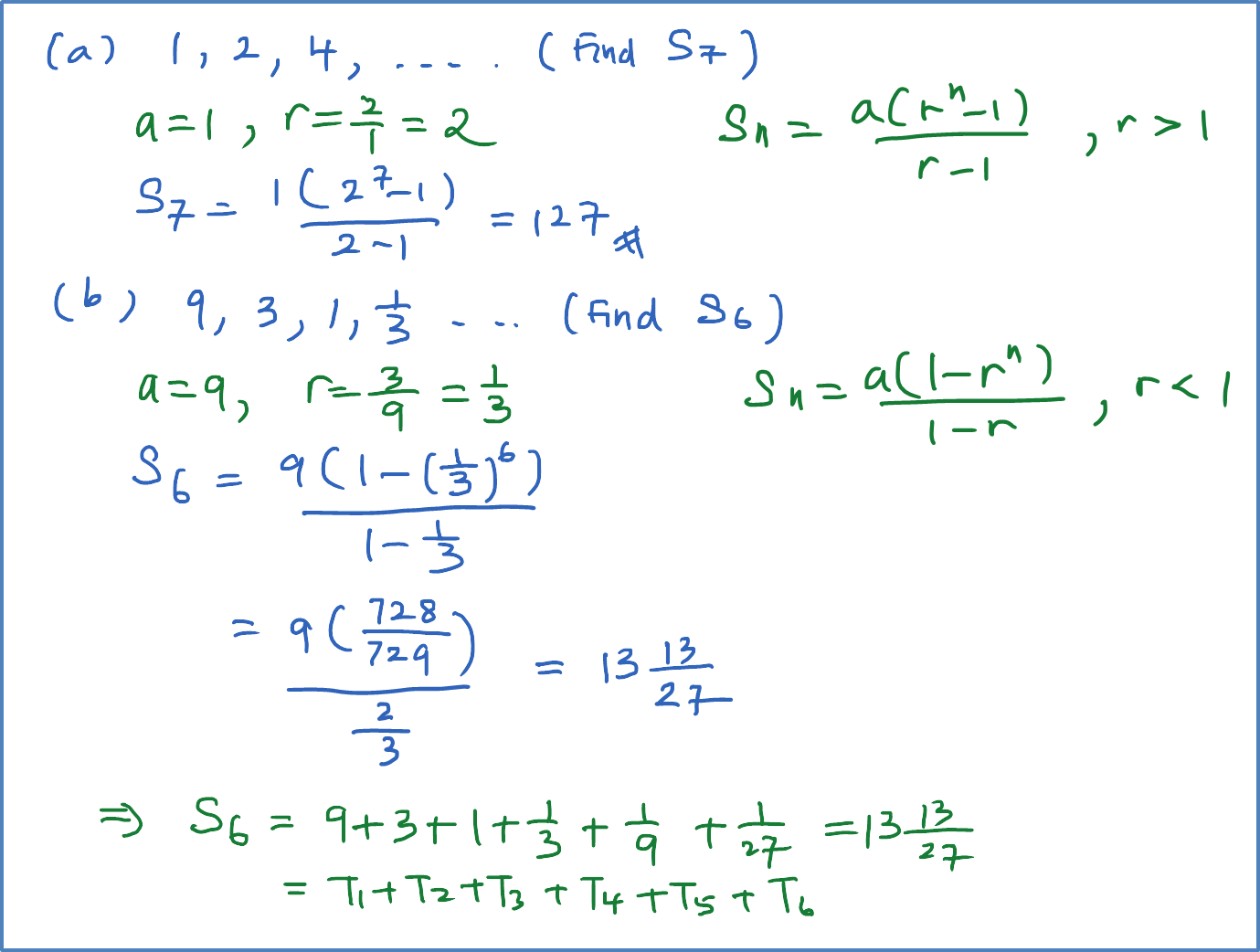

can i get the next link for sum to infinty of geo progressions